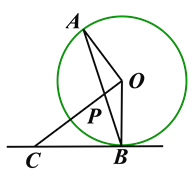
【题目】如图,AB是⊙O的弦,点C是在过点B的切线上,且OC⊥OA,OC交AB于点P.
(1)判断△CBP的形状,并说明理由;
(2)若⊙O的半径为6,AP=![]() ,求BC的长.
,求BC的长.
参考答案:
【答案】(1)△CBP是等腰三角形,理由见解析;(2)8.
【解析】【试题分析】(1)等腰三角形,理由:OC⊥OA,根据垂直的定义得![]() AOC=90°,根据三角形内角和定理∠A+∠APO=90°,因为BC切⊙O于点B,根据切线的性质,∠OBC=90°,即∠OBA+∠CBP=90°,因为OA=OB,根据等边对等角,得∠A=∠OBA,等量代换得,∠APO=∠CBP
AOC=90°,根据三角形内角和定理∠A+∠APO=90°,因为BC切⊙O于点B,根据切线的性质,∠OBC=90°,即∠OBA+∠CBP=90°,因为OA=OB,根据等边对等角,得∠A=∠OBA,等量代换得,∠APO=∠CBP
对等角相等得,∠APO=∠CPB,∠CPB=∠CBP,根据等角对等边得,CP=CB,即△CBP是等腰三角形;
(2)OC⊥OA,根据勾股定理得,OP=![]()
设BC=x,则OC=x+2,利用勾股定理得:![]() 即
即![]() ,解得x=8,即BC=8.
,解得x=8,即BC=8.
【试题解析】
等腰三角形,理由:
∵OC⊥OA,
∴∠AOC=90°,
∴∠A+∠APO=90°
∵BC切⊙O于点B,
∴∠OBC=90°,
∴∠OBA+∠CBP=90°
∵OA=OB,
∴∠A=∠OBA,
∴∠APO=∠CBP
∵∠APO=∠CPB,
∴∠CPB=∠CBP,
∴CP=CB
△CBP是等腰三角形;
(2)∵OC⊥OA,
∴OP=![]()
设BC=x,
∴OC=x+2,
∵![]()
∴![]() ,∴x=8,∴BC=8.
,∴x=8,∴BC=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全民健身和医疗保健是社会普遍关注的问题.2014年,某社区共投入30万元用于购买健身器材和药品.2015年,该社区购买健身器材的费用比上一年增加50%,购买药品的费用比上一年减少
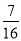 ,但社区在这两方面的总投入仍与2014年相同.
,但社区在这两方面的总投入仍与2014年相同.(1)求2014年社区购买药品的总费用;
(2)据统计,2014年该社区积极健身的家庭达到200户,但其药品费用明显减少,只占当年购买药品总费用的
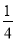 .与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的
.与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的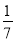 .求2015年该社区健身家庭的户数.
.求2015年该社区健身家庭的户数. -
科目: 来源: 题型:
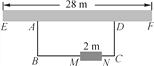
查看答案和解析>>【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△
 的外角
的外角 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)用等式表示线段
 ,
,  与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和同桌小聪在课后复习时,对下面的一道思考题进行了认真的探索.
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时点B到墙AC的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动________米.
解完【思考题】后,小聪提出了如下两个问题:
(1)在【思考题】中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(2)在【思考题】中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
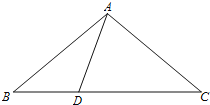
(1)若CD=CA=AB,请求出y与x的等量关系式;
(2)当D为边BC上一点,并且CD=CA,x=40,y=30时,则AB AC(填“=”或“≠”);
(3)如果把(2)中的条件“CD=CA”变为“CD=AB”,且x,y的取值不变,那么(1)中的结论是否仍成立?若成立请写出证明过程,若不成立请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:
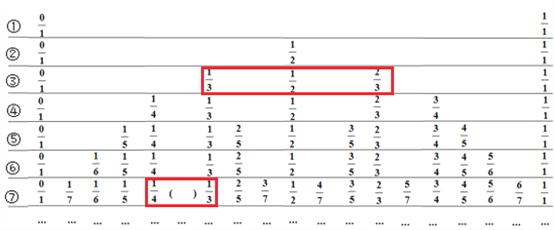
两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数
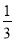 、
、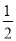 、
、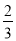 ,有
,有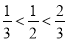 ,所以
,所以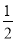 为
为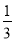 和
和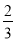 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到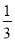 和
和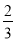 的中间分数
的中间分数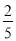 ,
, 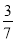 ,
, 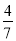 ,
, 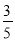 .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到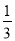 和
和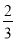 更多的中间分数.
更多的中间分数.(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的
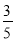 和
和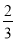 的中间分数是 ;
的中间分数是 ;(2)写出分数
 和
和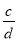 (a、b、c、d均为正整数,
(a、b、c、d均为正整数,  ,
, 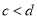 )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;(3)若
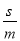 与
与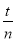 (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是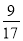 和
和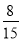 的中间分数,则
的中间分数,则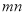 的最小值为 .
的最小值为 .
相关试题

