【题目】小明和同桌小聪在课后复习时,对下面的一道思考题进行了认真的探索.
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时点B到墙AC的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动________米.
解完【思考题】后,小聪提出了如下两个问题:
(1)在【思考题】中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(2)在【思考题】中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.

参考答案:
【答案】0.8.
【解析】试题分析:(1)(2)利用勾股定理判断即可.
试题解析:
(1)不会是0.9米.若AA1=BB1=0.9,则A1C=2.4-0.9=1.5,B1C=0.7+0.9=1.6,1.52+1.62=4.81,2.52=6.25,
∵A1C2+B1C2≠A1B,
∴该题的答案不会是0.9米.
(2)有可能.设梯子顶端从A处下滑x米,点B向外也移动x米,则有(x+0.7)2+(2.4-x)2=2.52.解得x=1.7或x=0(舍去).
∴当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.
-
科目: 来源: 题型:
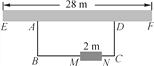
查看答案和解析>>【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△
 的外角
的外角 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)用等式表示线段
 ,
,  与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,点C是在过点B的切线上,且OC⊥OA,OC交AB于点P.
(1)判断△CBP的形状,并说明理由;
(2)若⊙O的半径为6,AP=
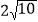 ,求BC的长.
,求BC的长.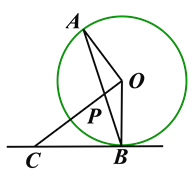
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
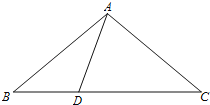
(1)若CD=CA=AB,请求出y与x的等量关系式;
(2)当D为边BC上一点,并且CD=CA,x=40,y=30时,则AB AC(填“=”或“≠”);
(3)如果把(2)中的条件“CD=CA”变为“CD=AB”,且x,y的取值不变,那么(1)中的结论是否仍成立?若成立请写出证明过程,若不成立请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:
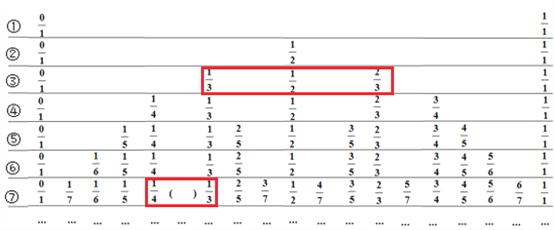
两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数
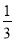 、
、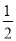 、
、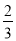 ,有
,有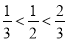 ,所以
,所以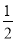 为
为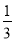 和
和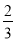 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到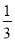 和
和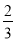 的中间分数
的中间分数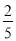 ,
, 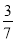 ,
, 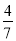 ,
, 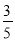 .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到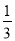 和
和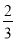 更多的中间分数.
更多的中间分数.(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的
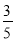 和
和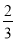 的中间分数是 ;
的中间分数是 ;(2)写出分数
 和
和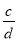 (a、b、c、d均为正整数,
(a、b、c、d均为正整数,  ,
, 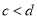 )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;(3)若
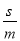 与
与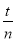 (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是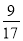 和
和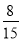 的中间分数,则
的中间分数,则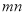 的最小值为 .
的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥DE,求证:∠D+∠BCD-∠B=180°.
证明:过点C作CF∥AB.
∵AB∥CF(已知),
∴∠B=________(____________________).
∵AB∥DE,CF∥AB(已知),
∴CF∥DE(__________________________________).
∴∠2+________=180°(________________________).
∵∠2=∠BCD-________(已知),
∴∠D+∠BCD-∠B=180°(等量代换).

相关试题

