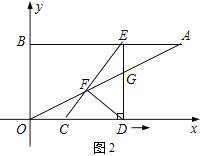
【题目】如图1,已知点A(8,4),点B(0,4),线段CD的长为3,点C与原点O重合,点D在x轴正半轴上.线段CD沿x轴正方向以每秒1个单位长度的速度向右平移,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F(如图2),设运动时间为t.当E点与A点重合时停止运动.
(1)求线段CE的长;
(2)记△CDE与△ABO公共部分的面积为S,求S关于t的函数关系式;
(3)如图2,连接DF.
①当t取何值时,以C、F、D为顶点的三角形为等腰三角形?
②△CDF的外接圆能否与OA相切?如果能,直接写出此时t的值;如果不能,请说明理由.

参考答案:
【答案】(1)5;(2)S=![]() (5-t )2(0≤t≤5);(3)①t=3或
(5-t )2(0≤t≤5);(3)①t=3或![]() 或
或 ![]() 时,△CDF为等腰三角形;②能 t=
时,△CDF为等腰三角形;②能 t=![]() .
.
【解析】分析:(1)、根据Rt△CDE的勾股定理求出CE的长度;(2)、作FH⊥CD于H,根据题意得出△OCF∽△AEF和△ODG∽△AEG,得出![]() 和
和![]() 的采购员CF和EG的长度,然后根据FH∥ED得出
的采购员CF和EG的长度,然后根据FH∥ED得出 ![]() ,从而求出HD的长度,最后根据S=
,从而求出HD的长度,最后根据S= ![]() EG·HD得出函数解析式;(3)、根据CF=CD、CF=DF和DF=CD三种情况分别求出t的值;作FH⊥CD于H得出△FCH∽△ECD,从而得出
EG·HD得出函数解析式;(3)、根据CF=CD、CF=DF和DF=CD三种情况分别求出t的值;作FH⊥CD于H得出△FCH∽△ECD,从而得出![]() ,然后求出
,然后求出![]() ,
,![]() ,
,![]() ,根据切割线定理得出OF2=OC
,根据切割线定理得出OF2=OC![]() OD,从而得出t的值.
OD,从而得出t的值.
详解:(1)在Rt△CDE中,CD=3,DE=4, ∴CE=![]() =5,
=5,

(2)作FH⊥CD于H,∵AB∥OD,∴△OCF∽△AEF,△ODG∽△AEG,
∴![]() ,
,![]() , 又∵CF+EF=5,DG+EG=4,∴CF=t,EG=
, 又∵CF+EF=5,DG+EG=4,∴CF=t,EG=![]() ,∵FH∥ED,∴
,∵FH∥ED,∴ ![]() ,∴HD=
,∴HD=![]() ·CD=
·CD=![]() (5-t )
(5-t )
∴S= ![]() EG·HD=
EG·HD=![]() ×
×![]() ×
×![]() (5-t )=
(5-t )=![]() (5-t )2(0≤t≤5)
(5-t )2(0≤t≤5)
(3)①由(2)知CF=t,(i)当CF=CD时,则t=3,(ii)当CF=DF时,则CH=![]() CD,
CD,

∵FH∥ED,∴CF= ![]() CE=
CE= ![]() ,∴t=
,∴t=![]() ;
;
(iii)当DF=CD时,作DK⊥CF于K,则CK=![]() CF=
CF=![]() t,
t,
∵CK=CD·cos∠ECD,∴![]() t=3×
t=3×![]() ,∴t=
,∴t=![]() ;
;
综上,当t=3或![]() 或
或 ![]() 时,△CDF为等腰三角形;
时,△CDF为等腰三角形;
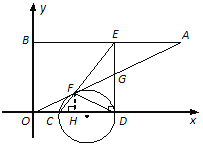
②能 t=![]() 作FH⊥CD于H,则△FCH∽△ECD,∴
作FH⊥CD于H,则△FCH∽△ECD,∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
若△CDF的外接圆与OA相切,则F点为切点, 由切割线定理,得:OF2=OC![]() OD,
OD,
∴![]() , 解得t=
, 解得t=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以O为圆心的弧BD度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
(1)求
 的值;
的值;(2)若OE与弧BD交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;(3)在(2)的条件下,若BC=1,求tan∠BCO的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校假期由校长带领该校“三好学生”去旅游,甲旅行社说“若校长买全票一张,则学生半价.”乙旅行社说“全部人六折优惠”若全票价是1200元,则:
(1)若学生人数是20人,甲、乙旅行社收费分别是多少?
(2)当学生人数的多少时,两家旅行社的收费一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税;
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税.
试根据上述纳税的计算方法作答:
(1)若王老师获得的稿费为2400元,则应纳税 元,若王老师获得的稿费为4000元,则应纳税 元;
(2)若王老师获稿费后纳税420元,求这笔稿费是多少元?
-
科目: 来源: 题型:
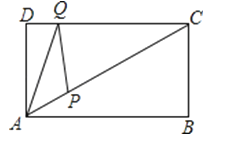
查看答案和解析>>【题目】如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是( )
A. 有理数就是正数和负数 B. 没有最小的有理数
C. 任何两个有理数一定可以进行加减乘除运算 D. 在
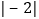 ,
,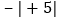 ,
,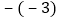 ,
,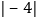 ,
,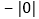 ,
,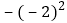 中,负数共有
中,负数共有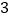 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】按照规律填上所缺的单项式并回答问题:
(1)a、﹣2a2、3a3、﹣4a4, , ;
(2)试写出第2007个单项式 ;第2008个单项式 ;
(3)试写出第n个单项式 .
相关试题

