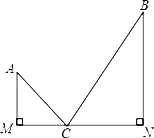
【题目】如图:已知:![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,点
,点![]() 是
是![]() 上使
上使![]() 的值最小的点.若
的值最小的点.若![]() ,
,![]() ,
,![]() ,则
,则![]() ________.
________.
参考答案:
【答案】![]()
【解析】
以MN为对称轴作A点对称点A′,连接A′B交MN于C,则A′B就是AC+BC最小值,延长BN使ND=A′M,连接A′D;
根据矩形的判定得到四边形A′DNM是矩形,由矩形的性质得ND,A′D的长,在Rt△A′BD中运用勾股定理求得A′B的长,即可求得AC+BC的最小值.
解:
作A点关于直线MN的对称点A′,连接A′B交MN于C,
则AC+BC=A′C+BC=A′B,
A′B就是AC+BC的最小值;
延长BN使ND=A′M,连接A′D,
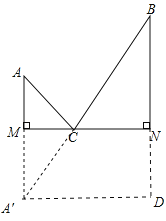
∵AM⊥MN,BN⊥MN,
∴AA′∥BD.
∵ND=A′M,
∴四边形A′DNM是平行四边形,
∵AM⊥MN,
∴∠AMC=90°,
∴∠A′MC=90°,
∴四边形A′DNM是矩形,
∴ND=AM=3,A′D=MN=15,
∴BD=BN+ND=5+3=8,
∴A′B=![]() ,
,
∴AC+BC=17.
故答案为:17.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(a,1)、B(-1,b)的坐标满足:
 .
.(1)直接写出点A、B的坐标;
(2)如图,过点E(m,0)(m>1)作x轴的垂线l1,点A关于l1的对称点为A’(2m-1,1),若BA’交x轴于点F,当E点在x轴上运动时,求EF的长度;
(3)如图,把点A向上平移2个单位到点C,过点C作y轴的垂线l2,点D(n,c)在直线l2上(不和C重合),若∠CDA=
 ,连接OA、DA,∠AOx=45°,若满足∠DAO=225°-
,连接OA、DA,∠AOx=45°,若满足∠DAO=225°- ,求n的取值范围.
,求n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.
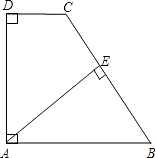
(1)求证:AD=AE;
(2)若AD=8,DC=4,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是腰长为1的等腰三角形,以
是腰长为1的等腰三角形,以 的斜边
的斜边 为直角边,画第二个等腰三角形
为直角边,画第二个等腰三角形 ,再以
,再以 的斜边
的斜边 为直角边,画第三个等腰三角形
为直角边,画第三个等腰三角形 ,…,以此类推,则第2019个等腰三角形的斜边长是___________。
,…,以此类推,则第2019个等腰三角形的斜边长是___________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,AB为⊙O的直径,连结BD.若∠BCD=120°,则∠ABD的大小为( )
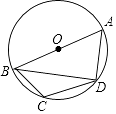
A.60°
B.50°
C.40°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】小强家有一块三角形菜地,量得两边长分别为
 ,
, ,第三边上的高为
,第三边上的高为 .请你帮小强计算这块菜地的面积.(结果保留根号)
.请你帮小强计算这块菜地的面积.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l所对应的函数表达式为y=x.过点A1(0,1)作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;过点A2作y轴的垂线交直线l于点B2 , 则点B2的坐标为( )
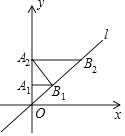
A.(1,1)
B.(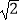 ,
, 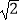 )
)
C.(2,2)
D.(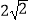 ,
, 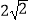 )
)
相关试题

