【题目】操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C'处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=3,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:如图3,当点P在线段EF的延长线上运动时,若DE=a,CF=b.请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)

参考答案:
【答案】(1)证明见解析;(2)8;(3)QN﹣QM=![]() .
.
【解析】
(1)证明∠BEF=∠BFE即可解决问题(也可以利用全等三角形的性质解决问题即可).
(2)如图2中,连接BP,作EH⊥BC于H,则四边形ABHE是矩形.利用等面积法证明PM+PN=EH,利用勾股定理求出AB即可解决问题.
(3)如图3中,连接BP,作EH⊥BC于H.由S△EBPS△BFP=S△EBF,可得![]() BEPM
BEPM![]() BFPN=
BFPN=![]() BFEH,由BE=BF,推出PMPN=EH=
BFEH,由BE=BF,推出PMPN=EH=![]() ,即可得到QNQM=PMPN=
,即可得到QNQM=PMPN=![]() .
.
(1)如图1中,

∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠EFB,
由翻折可知:∠DEF=∠BEF,
∴∠BEF=∠EFB,
∴BE=BF;
(2)如图2中,连接BP,作EH⊥BC于H,则四边形ABHE是矩形,EH=AB,

∵DE=EB=BF=5,CF=3,
∴AD=BC=8,AE=3,
在Rt△ABE中,∵∠A=90°,BE=5,AE=3,
∴AB=![]() ,
,
∵S△BEF=S△PBE+S△PBF,PM⊥BE,PN⊥BF,
∴![]() BFEH=
BFEH=![]() BEPM+
BEPM+![]() BFPN.
BFPN.
∵BE=BF,
∴PM+PN=EH=4.
∵四边形PMQN是平行四边形,
∴四边形PMQN的周长=2(PM+PN)=8;
(3)如图3中,连接BP,作EH⊥BC于H.

∵ED=EB=BF=a,CF=b,
∴AD=BC=a+b,
∴AE=ADDE=b,
∴EH=AB=![]() ,
,
∵S△EBPS△BFP=S△EBF,
∴![]() BEPM
BEPM![]() BFPN=
BFPN=![]() BFEH,
BFEH,
∵BE=BF,
∴PMPN=EH=![]() ,
,
∵四边形PMQN是平行四边形,
∴QNQM=PMPN=![]() .
.
-
科目: 来源: 题型:
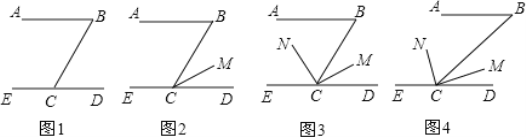
查看答案和解析>>【题目】 (1)①如图1,已知AB∥CD,∠ABC=60°,可得∠BCD=_______°;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM=_________°;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN=___________°.
(2)、尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线, CN⊥CM,求∠BCM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】书店老板去图书批发市场购买某种图书,第一次用1200元购买若干本,很快售完.第二次购买时,每本书的进价比第一次提高了20%,他用1500元所购买的数量比第一次多10本.求第一次购买的图书,每本进价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为矩形,点E是边BC的中点,AF∥ED,AE∥DF
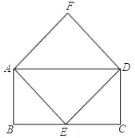
(1)求证:四边形AEDF为菱形;
(2)试探究:当AB:BC= ,菱形AEDF为正方形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,
, 由
由 绕点
绕点 顺时针旋转得到,其中点
顺时针旋转得到,其中点 与点
与点 、点
、点 与点
与点 是对应点,连接
是对应点,连接 ,且
,且 、
、 、
、 在同一条直线上,则
在同一条直线上,则 的长为( )
的长为( )
A. 3 B.
 C. 4 D.
C. 4 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点和该抛物线与y轴的交点在一次函数y=kx+1(k≠0)的图象上,它的对称轴是x=1,有下列四个结论:①abc<0,②a<﹣
 ,③a=﹣k,④当0<x<1时,ax+b>k,其中正确结论的个数是( )
,③a=﹣k,④当0<x<1时,ax+b>k,其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字1,2,3,4,B布袋中有三个除标号外完全相同的小球,小球上分别标有数字2,4,6.小明先从A布袋中随机取出﹣个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)若用(m,n)表示小明取球时m与n 的对应值,请画出树形图或列表写出(m,n)的所有取值;
(2)求关于x的一元二次方程x2﹣mx+
 n=0有实数根的概率.
n=0有实数根的概率.
相关试题

