【题目】如图,△ABC内接于⊙O,AB、CD为⊙O直径,DE⊥AB于点E,sinA= ![]() ,则∠D的度数是 .
,则∠D的度数是 . 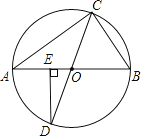
参考答案:
【答案】30°
【解析】解:∵AB为⊙O直径,
∴∠ACB=90°(直径所对的圆周角是直角);
又∵sinA= ![]() ,
,
∴∠CAB=30°,
∴∠ABC=60°(直角三角形的两个锐角互余);
又∵点O是AB的中点,
∴OC=OB,
∴∠OCB=OBC=60°,
∴∠COB=60°,
∴∠EOD=∠COB=60°(对顶角相等);
又∵DE⊥AB,
∴∠D=90°﹣60°=30°.
故答案是:30°.
由圆周角定理、特殊角的三角函数值求得∠CAB=30°;然后根据直角三角形的两个锐角互余的性质、等腰三角形的性质、对顶角相等求得∠EOD=∠COB=60°;最后在直角三角形ODE中求得∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活与数学
(1)吉姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是32,那么第一个数是 ;

(2)玛丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是 ;

(3)莉莉也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是 ;

(4)某月有5个星期日的和是75,则这个月中最后一个星期日是 号;
(5)若干个偶数按每行8个数排成下图:
①图中方框内的9个数的和与中间的数的关系是 ;

②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是 ;

③托马斯也画了一个斜框,斜框内9个数的和为252,则斜框的中间一个数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点距离AB=|a﹣b|.已知数轴上两点A,B对应的数分别为-1,3.点P为数轴上一动点,其对应的数为x,A,B两点之间的距离是 .设点P在数轴上表示的数为x,则x与-4之间的距离表示为 .
.若点P到点A、点B的距离相等,则点P对应的数为 .
若点P到点A、点B的距离之和为8,则点P对应的数为 .
现在点A以2个单位长度/秒的速度向右运动,同时点B以0.5个单位长度/秒的速度向左运动,当点A与点B之间的距离为3个单位长度时,求点A所对应的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c<0;③ac>0;④b2﹣4ac>0.其中正确的结论是( )
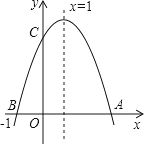
A.①④
B.①③
C.②④
D.①② -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=
 .
.
如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于 .
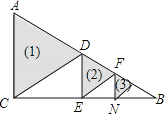
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP,求证:FP=EP.

相关试题

