【题目】如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP,求证:FP=EP.
参考答案:
【答案】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DGC=∠GCB(两直线平行,内错角相等),
∵DG=DC,
∴∠DGC=∠DCG,
∴∠DCG=∠GCB,
∵∠DCG+∠DCP=180°,∠GCB+∠FCP=180°,
∴∠DCP=∠FCP,
∵在△PCF和△PCE中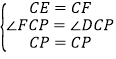 ,
,
∴△PCF≌△PCE(SAS),
∴PF=PE.
【解析】根据平行四边形的性质推出∠DGC=∠GCB,根据等腰三角形性质求出∠DGC=∠DCG,推出∠DCG=∠GCB,根据等角的补角相等求出∠DCP=∠FCP,根据SAS证出△PCF≌△PCE即可.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和平行四边形的性质的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB、CD为⊙O直径,DE⊥AB于点E,sinA=
 ,则∠D的度数是 .
,则∠D的度数是 . 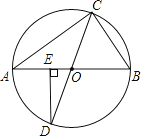
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=
 .
.
如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于 .
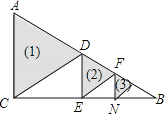
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某河的两岸PQ、MN互相平行,河岸PQ上的点A处和点B处各有一棵大树,AB=30米,某人在河岸MN上选一点C,AC⊥MN,在直线MN上从点C前进一段路程到达点D,测得∠ADC=30°,∠BDC=60°,求这条河的宽度.(
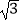 ≈1.732,结果保留三个有效数字).
≈1.732,结果保留三个有效数字).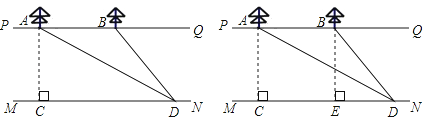
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有两个不透明的乒乓球盒,甲盒中装有1个白球和2个红球,乙盒中装有2个白球和若干个红球,这些小球除颜色不同外,其余均相同.若从乙盒中随机摸出一个球,摸到红球的概率为
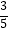 .
.
(1)求乙盒中红球的个数;
(2)若先从甲盒中随机摸出一个球,再从乙盒中随机摸出一个球,请用树形图或列表法求两次摸到不同颜色的球的概率.
相关试题

