【题目】2012义乌市)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 . 
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1 , CC1 . 若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1 , 求线段EP1长度的最大值与最小值.
参考答案:
【答案】
(1)解:由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°
(2)解:∵△ABC≌△A1BC1,
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴ ![]() ,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
∴∠ABA1=∠CBC1,
∴△ABA1∽△CBC1.
∴ ![]() ,
,
∵S△ABA1=4,
∴S△CBC1= ![]()
(3)解:①如图1,
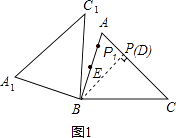
过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°= ![]() ,
,
当P在AC上运动,BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE= ![]() ﹣2;
﹣2;
②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+BE=2+5=7
【解析】(1)由由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1 , 又由等腰三角形的性质,即可求得∠CC1A1的度数;(2)由△ABC≌△A1BC1 , 易证得△ABA1∽△CBC1 , 然后利用相似三角形的面积比等于相似比的平方,即可求得△CBC1的面积;(3)由①当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,即可求得线段EP1长度的最大值与最小值.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
 是
是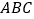 的边
的边 上的高,且
上的高,且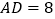 cm,
cm,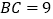 cm,点
cm,点 从点
从点 出发,沿线段
出发,沿线段 向终点
向终点 运动,其速度与时间的关系如图②所示,设点
运动,其速度与时间的关系如图②所示,设点 的运动时间为
的运动时间为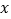 (s),
(s),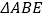 的面积为
的面积为 (cm2 ).
(cm2 ).(1)在点
 沿
沿 向点
向点 运动的过程中,它的速度是 cm/s,用含
运动的过程中,它的速度是 cm/s,用含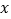 的代数式表示线段
的代数式表示线段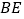 的长是 cm,变量
的长是 cm,变量 与
与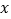 之间的函数表达式为;
之间的函数表达式为;(2)当
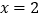 时,求
时,求 的值.当
的值.当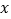 每增加1时,求
每增加1时,求 的变化情况.
的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.

(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB内部有顺次的四条射线:OE、OC、OD、OF、OE平分∠AOC,OF平分∠DOB.
(1)若∠AOB=160°,∠COD=40°,求∠EOF的度数;
(2)若∠AOB=a,∠COD=β,求∠EOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
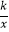 (x>0)的图象与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,若OC=2BD,则实数k的值为( )
(x>0)的图象与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,若OC=2BD,则实数k的值为( ) 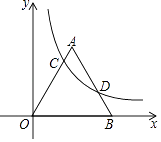
A.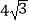
B.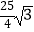
C.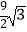
D.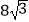
-
科目: 来源: 题型:
查看答案和解析>>【题目】平安加气站某日8:00的储气量为10 000立方米.从8:00开始,3把加气枪同时以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.8:30时,为缓解排队压力,又增开了2把加气枪.假设加气过程中每把加气枪加气的速度是匀速的,在不关闭加气枪的情况下,加气站的储气量
 (立方米)与时间
(立方米)与时间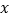 (小时)之间的函数关系如图中的折线
(小时)之间的函数关系如图中的折线 所示.
所示.(1)分别求出8:00 ~8:30及8:30之后加气站的储气量
 (立方米)与时间
(立方米)与时间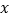 (小时)之间的函数表达式.
(小时)之间的函数表达式.(2)前30辆车能否在当天8:42之前加完气?
(3)若前
 辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求
辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求 的值.
的值.
相关试题

