【题目】如图①, ![]() 是
是![]() 的边
的边![]() 上的高,且
上的高,且![]() cm,
cm,![]() cm,点
cm,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,其速度与时间的关系如图②所示,设点
运动,其速度与时间的关系如图②所示,设点![]() 的运动时间为
的运动时间为![]() (s),
(s),![]() 的面积为
的面积为![]() (cm2 ).
(cm2 ).
(1)在点![]() 沿
沿![]() 向点
向点![]() 运动的过程中,它的速度是 cm/s,用含
运动的过程中,它的速度是 cm/s,用含![]() 的代数式表示线段
的代数式表示线段![]() 的长是 cm,变量
的长是 cm,变量![]() 与
与![]() 之间的函数表达式为;
之间的函数表达式为;
(2)当![]() 时,求
时,求![]() 的值.当
的值.当![]() 每增加1时,求
每增加1时,求![]() 的变化情况.
的变化情况.

参考答案:
【答案】(1)3cm/s, ![]() 的长是
的长是![]() cm,
cm,![]() ;(2)
;(2) ![]() =24.当
=24.当![]() 每增加1时,
每增加1时,![]() 增加12.
增加12.
【解析】
(1)根据图2即可求得点E沿BC向点C运动的过程中的速度,根据速度、路程和时间的关系即可求得BE的长,进而根据三角形面积公式求得y与x的关系式;
(2)把x=2代入关系式即可求得y的值,直线的斜率就是函数的变化率.
解:

(1)由图2可知,在点E沿BC向点C运动的过程中,它的速度是3cm/s,
所以线段BE的长是3xcm;
根据三角形的面积公式得:y=![]() ×3x×8=12x;
×3x×8=12x;
(2)当x=2时,y=12×2=24;
由y=12x可知,因为12是斜率,说明x每增加一个单位,y增加12个单位,
所以当x每增加1s时,y增加12cm2,
故答案为: (1)3cm/s; ![]() 的长是
的长是![]() cm;
cm; ![]() ;(2)
;(2) ![]() =24;当
=24;当![]() 每增加1时,
每增加1时,![]() 增加12.
增加12.
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.

(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在烧开水时,水温达到100℃就会沸腾,下表是某同学做“观察水的沸腾”实验时记录的数据:

(1)上表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间推移2分钟,水的温度如何变化?
(4)时间为8分钟时,水的温度为多少?你能得出时间为9分钟时,水的温度吗?
(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
-
科目: 来源: 题型:
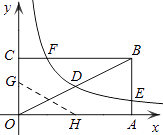
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数
 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=  .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.

(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB内部有顺次的四条射线:OE、OC、OD、OF、OE平分∠AOC,OF平分∠DOB.
(1)若∠AOB=160°,∠COD=40°,求∠EOF的度数;
(2)若∠AOB=a,∠COD=β,求∠EOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2012义乌市)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 .

(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1 , CC1 . 若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1 , 求线段EP1长度的最大值与最小值.
相关试题

