【题目】若△ABC中,AB=13,BC=5,AC=12,则下列判断正确的是( )
A.∠A=90°B.∠B=90°
C.∠C=90°D.△ABC是锐角三角形
参考答案:
【答案】C
【解析】
13,12,5正好是一组勾股数,根据勾股定理的逆定理即可判断△ABC是直角三角形,从而求解.
∵52+122=169,132=169,
∴52+122=132,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°.
故选:C.
-
科目: 来源: 题型:
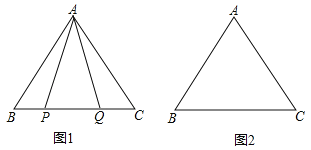
查看答案和解析>>【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
-
科目: 来源: 题型:
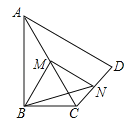
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列横线上用含有a,b的代数式表示相应图形的面积.
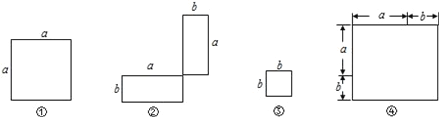
① ; ② ; ③ ; ④ .
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示: ;
(3)利用(2)的结论计算972+2×97×3+32的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+kxy+64y2是一个完全平方式,则k的值是( )
A.8
B.±8
C.16
D.±16 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD=4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是c,且|a+8|与(c﹣16)2互为相反数.
温馨提示:忽略两辆火车的车身及双铁轨的宽度.

(1)求此时刻快车头A与慢车头C之间相距 单位长度.
(2)从此时刻开始,若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,再行驶 秒两列火车的车头A、C相距8个单位长度.
(3)在(2)中快车、慢车速度不变的情况下,此时在快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟內,他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值(即PA+PC+PB+PD为定值).则这段时间t是 秒,定值是 单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A. 三点确定一个圆B. 有一个角是直角的四边形是矩形
C. 菱形的对角线互相平分且相等D. 相似三角形的对应角相等、对应边成比例
相关试题

