【题目】在学习绝对值后,我们知道,![]() 表示数a在数轴上的对应点与原点的距离,如:5表示5在数轴上的对应点到原点的距离.而
表示数a在数轴上的对应点与原点的距离,如:5表示5在数轴上的对应点到原点的距离.而![]() ,即
,即![]() 表示5、0在数轴上对应的两点之间的距离,类似的,有:
表示5、0在数轴上对应的两点之间的距离,类似的,有:![]() 表示5、3在数轴上对应的两点之间的距离;
表示5、3在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示5、-3在数轴上对应的两点之间的距离一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为
表示5、-3在数轴上对应的两点之间的距离一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为![]() .
.
请根据绝对值的意义并结合数轴解答下列问题:
(1)数轴上表示2和3的两点之间的距离是________;数轴上P、Q两点的距离为3,点P表示的数是2,则点Q表示的数是________.
(2)点A、B、C在数轴上分别表示有理数x、-3、1,那么A到B的距离与A到C的距离之和可表示为________(用含绝对值的式子表示);满足![]() 的x的值为________;
的x的值为________;
(3)试求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)1;5或-1;(2)![]() ;-3或4;(3)2500
;-3或4;(3)2500
【解析】
(1)根据在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为![]() ,代入即可求解;
,代入即可求解;
(2)根据数轴上两点之间的距离公式可得A到B的距离与A到C的距离;满足![]() 中x的值分三种情况讨论即可求解;
中x的值分三种情况讨论即可求解;
(3)把![]()
化为![]()
分别求出![]() 、
、![]() …
…![]() 在50≤x≤51时去最小值即可求解.
在50≤x≤51时去最小值即可求解.
(1)数轴上表示2和3的两点之间的距离是3-2=1;
数轴上P、Q两点的距离为3,点P表示的数是2,则点Q表示的数是2-3=-1或2+3=5;
(2)A到B的距离与A到C的距离之和可表示为![]() ;
;
∵![]()
当x<-2时,3-x-x-2=7 ,解得x=-3
当-2≤x≤3,x不存在
当x>3时,x-3+x+2=7,解得x=4
故满足![]() 的x的值为-3或4;
的x的值为-3或4;
(3)![]() =
=![]()
当1≤x≤100,![]() 有最小值为
有最小值为![]() =99;
=99;
当2≤x≤99,![]() 有最小值为
有最小值为![]() =97;
=97;
...
当50≤x≤51,![]() 有最小值为
有最小值为![]() =1;
=1;
∴当50≤x≤51,![]() 有最小值为99+97+95+…+3+1=(99+1)+(97+3)+(95+5)+…+(51+49)=100×25=2500.
有最小值为99+97+95+…+3+1=(99+1)+(97+3)+(95+5)+…+(51+49)=100×25=2500.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+bx+c的图象经过点(0,2)和(1,﹣1),求图象的顶点坐标和对称轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小区:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据
成绩x(分)
60≤x≤70
70<x≤80
80<x≤90
90<x≤100
甲小区
2
5
a
b
乙小区
3
7
5
5
分析数据
统计量
平均数
中位数
众数
甲小区
85.75
87.5
c
乙小区
83.5
d
80
应用数据
(1)填空:a= ,b= ,c= ,d= ;
(2)若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下几个图形是五角星和它的变形.

(1)图甲是一个五角星 ABCDE,则∠A+∠B+∠C+∠D+∠E 的度数为 ;(不必 写过程)
(2)如图乙,如果点 B 向右移动到 AC 上时,则∠A+∠EBD+∠C+∠D+∠E 度数为 ;(不必写过程)
(3)如图丙,点 B 向右移动到 AC 的另一侧时,(1)的结论成立吗?为什么?
(4)如图丁,点 B,E 移动到∠CAD 的内部时,结论又如何?(不必写过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,小明在玩纸片拼图游戏时,发现利用图①中的三种材料各若干,可以拼出一些长方形来解释某些等式,比如图②可以解释为等式:
 .
.
(1)则图③可以解释为等式: .
(2)在虚线框中用图①中的基本图形若干块(每种至少用一次)拼成一个长方形,使拼出的长方形面积为
 ,并请在图中标出这个长方形的长和宽.
,并请在图中标出这个长方形的长和宽.(3)如图④,大正方形的边长为
 ,小正方形的边长为
,小正方形的边长为 ,若用
,若用 、
、 表示四个长方形的两边长(
表示四个长方形的两边长( ),观察图案,指出以下关系式:(
),观察图案,指出以下关系式:( )
) ;(
;( )
)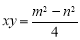 ;(
;(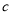 )
) ; (
; ( )
) .其中正确的关系式的个数有 个.
.其中正确的关系式的个数有 个. -
科目: 来源: 题型:
查看答案和解析>>【题目】李大爷一年前买入了A、B两种兔子共46只.目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只.
(1)则一年前李大爷买入A种兔子________只,目前A、B两种兔子共________只(用含a的代数式表示);
(2)若一年前买入的A种兔子数量多于B种兔子数量,则目前A、B两种兔子共有多少只?
(3)李大爷目前准备卖出30只兔子,已知卖A种兔子可获利15元/只,卖B种兔子可获利6元/只.如果卖出的A种兔子少于15只,且总共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?请求出最大获利.
相关试题

