【题目】如图,已知函数y=ax2+bx+c ![]() 的图象如图所示,有以下四个结论:①abc=0,②
的图象如图所示,有以下四个结论:①abc=0,② ![]() ,③
,③ ![]() ,④
,④ ![]() ;其中正确的结论有( )
;其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】∵二次函数y=ax2+bx+c图象经过原点,
∴c=0,
∴abc=0,①符合题意;
∵x=1时,y<0,
∴a+b+c<0,②不符合题间;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴是x= ![]() ,
,
∴ ![]() ,
,
∴b=3a,
又∵a<0,b<0,
∴a>b,③符合题意;
∵二次函数y=ax2+bx+c图象与x轴有两个交点,
∴△>0,
∴b2-4ac>0,4ac-b2<0,④符合题意;
综上可得正确结论有3个:①③④.
故答案为:C.
由抛物线开口方向得到a<0以及函数经过原点即可判断①,由抛物线的对称轴方程得到为b=2a<0,以及a的符号即可判断③;根据x=1时的函数值可以判断②;根据抛物线与x轴交点个数得到△=b2-4ac>0,则可对④进行判断.本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile,它们离开港口一个半小时后相距30nmile,且知道“远航”号沿东北方向航行,那么“海天”号航行的方向是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市2018年举行迎新春首届灯展,承办方计划在现场安装小彩灯和大彩灯,已知:安装5个小彩灯和4个大彩灯共需155元;安装7个小彩灯和6个大彩灯共需225元.
(1)安装1个小彩灯和1个大彩灯各需多少元.
(2)若承办方安装小彩灯和大彩灯的数量共300个,费用不超过5000元,则最多安装大彩灯多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进价为
 元∕件的玩具以
元∕件的玩具以  元∕件的价格出售时,每天可售出
元∕件的价格出售时,每天可售出  件,经调查当单价每涨
件,经调查当单价每涨  元时,每天少售出
元时,每天少售出  件.若商场想每天获得
件.若商场想每天获得  元利润,则每件玩具应涨多少元?若设每件玩具涨
元利润,则每件玩具应涨多少元?若设每件玩具涨  元,则下列说法错误的是( )
元,则下列说法错误的是( )
A.涨价后每件玩具的售价是 元
元
B.涨价后每天少售出玩具的数量是 件
件
C.涨价后每天销售玩具的数量是 件
件
D.可列方程为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
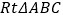 中,
中, 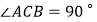 ,
, 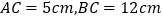 ,将
,将 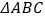 绕点
绕点 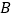 顺时针旋转
顺时针旋转 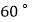 ,得到
,得到 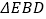 ,连接
,连接 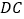 ,交
,交 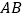 于点
于点 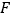 ,则
,则 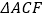 与
与 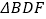 的周长之和为
的周长之和为  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房. 如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?
相关试题

