【题目】如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile,它们离开港口一个半小时后相距30nmile,且知道“远航”号沿东北方向航行,那么“海天”号航行的方向是_______.

参考答案:
【答案】西北方向
【解析】根据路程=速度×时间分别求得PQ、PR的长,再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形,从而求解.
解:根据题意,得
PQ=16×1.5=24(海里),PR=12×1.5=18(海里),QR=30(海里).
∵242+182=302,
即PQ2+PR2=QR2,
∴∠QPR=90°.
由“远航号”沿东北方向航行可知,∠QPS=45°,则∠SPR=45°,
即“海天”号沿西北方向航行.
“点睛”此题主要是能够根据勾股定理的逆定理发现直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=
 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.
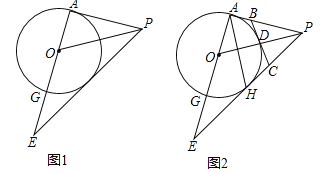
(1)求证:直线PE是⊙O的切线;
(2)在图2中,设PE与⊙O相切于点H,连结AH,点D是⊙O的劣弧
 上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=
上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=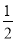 ,求EH的长.
,求EH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】 菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为( )
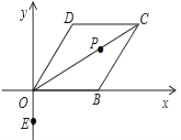
A.(2
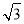 -3,2-
-3,2-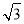 )
)B.(2
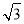 +3, 2-
+3, 2-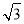 )
) C.(2
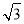 -3, 2+
-3, 2+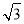 )
) D.(2
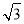 +3, 2+
+3, 2+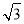 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中不是方程的是( )
A. 2x+3y=1 B. -x+y=4
C. 3π+4≠5 D. x=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】x2x3的计算结果是( )
A. x5 B. x6 C. x8 D. x9
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式变形不正确的是( )
A. 由x=y,得到x+2=y+2
B. 由2a﹣3=b﹣3,得到2a=b
C. 由m=n,得到2am=2an
D. 由am=an,得到m=n
相关试题

