【题目】如图,二次函数 ![]() 的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
(1)求二次函数解析式;
(2)直线![]() 与
与![]() 轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
①求线段PF取得最大值时,OE的长;
②四边形ACPB的面积是否存在最大值?如果存在求出此最大值和点P的坐标;如果不存在,说明理由.
(3)不解方程组,直接写出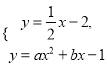 的解.
的解.

参考答案:
【答案】(1)![]() (2)①1;
(2)①1; ![]() (3)
(3)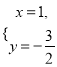
【解析】分析:(1)由△AOC∽△COB得:OA=![]() ,则点A(-
,则点A(-![]() ,0),把A、B代入联立方程组,即可求解;(2)①由题意得到直线BC的解析式为:
,0),把A、B代入联立方程组,即可求解;(2)①由题意得到直线BC的解析式为: ![]() ,分别设出点E、F、P的坐标,用含m的式子表示,从而求出线段PF取得最大值时,OE的长;
,分别设出点E、F、P的坐标,用含m的式子表示,从而求出线段PF取得最大值时,OE的长;
②利用![]() ,得到关于m的二次函数,配成顶点式,即可求解;(4)根据函数图象可得出结果.
,得到关于m的二次函数,配成顶点式,即可求解;(4)根据函数图象可得出结果.
本题解析:
(1)∵∠ACB=90o, ![]() ,∴
,∴![]()
∴![]() ,∴点A的坐标为
,∴点A的坐标为![]()
∴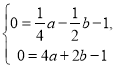 ∴
∴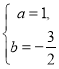
∴![]()
(2)①设直线BC的解析式为![]() ,由图象得:
,由图象得:
![]() , ∴
, ∴![]()
∴直线BC的解析式为: ![]() .
.
如图,设:E![]() ,则F
,则F![]() ,p
,p![]() ,
,
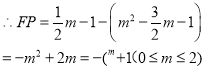
∴当m=1时, ![]()
∴OE=1
② 如图:
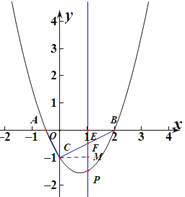
四边形ACPB的面积存在最大值,
![]()
=![]() ,
,
![]() ,
,
∴P(1, ![]() ).
).
(3)由图可知:
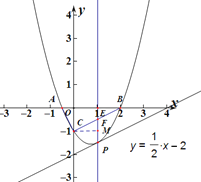
方程组: 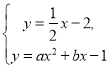 的解为
的解为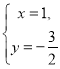
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a3a=6a
B.(﹣a3)2=a6
C.6a÷2a=3a
D.(﹣2a)3=﹣6a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
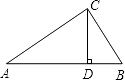
(1)求DC的长.
(2)求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果水库水位上升2m记作+2m,那么水库水位下降6m记作_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,一只蚂蚁从原点出发,先向右爬行了4个单位长度到达点A,再向右爬行了2个单位长度到达点B,然后又向左爬行了10个单位长度到达点C.
(1)画出数轴,并在数轴上表示出A、B、C三点;
(2)根据点C在数轴上的位置,点C可以看作是蚂蚁从原点出发,向哪个方向爬行了几个单位长度得到的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(x﹣2)2+1的图象的对称轴为_____.顶点坐标是_____.与y轴交点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂工业废气年排放量为400万立方米,为改善大气环境质量,决定分二期投入治理,使废气的年排放量减少到256万立方米,如果每期治理中废气减少的百分率相同.求每期减少的百分率是多少?
相关试题

