【题目】如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9. 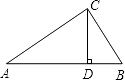
(1)求DC的长.
(2)求AB的长.
参考答案:
【答案】
(1)解:∵CD⊥AB于D,且BC=15,BD=9,AC=20
∴∠CDA=∠CDB=90°
在Rt△CDB中,CD2+BD2=CB2,
∴CD2+92=152
∴CD=12
(2)解:在Rt△CDA中,CD2+AD2=AC2
∴122+AD2=202
∴AD=16,
∴AB=AD+BD=16+9=25
【解析】(1)由题意可知三角形CDB是直角三角形,利用已知数据和勾股定理直接可求出DC的长;(2)有(1)的数据和勾股定理求出AD的长,进而求出AB的长.
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m﹣2014的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于多项式3x3y﹣4zy4+2x2y﹣1,下面说法正确的是( )
A.项分别是3x3y,4xy4 , 2x2y
B.多项式的次数是4次
C.按x的升幂排列是1﹣4xy4+2x2y+3x3y
D.这是个5次4项式 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a3a=6a
B.(﹣a3)2=a6
C.6a÷2a=3a
D.(﹣2a)3=﹣6a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果水库水位上升2m记作+2m,那么水库水位下降6m记作_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
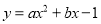 的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.(1)求二次函数解析式;
(2)直线
 与
与 轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.①求线段PF取得最大值时,OE的长;
②四边形ACPB的面积是否存在最大值?如果存在求出此最大值和点P的坐标;如果不存在,说明理由.
(3)不解方程组,直接写出
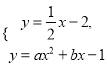 的解.
的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,一只蚂蚁从原点出发,先向右爬行了4个单位长度到达点A,再向右爬行了2个单位长度到达点B,然后又向左爬行了10个单位长度到达点C.
(1)画出数轴,并在数轴上表示出A、B、C三点;
(2)根据点C在数轴上的位置,点C可以看作是蚂蚁从原点出发,向哪个方向爬行了几个单位长度得到的?
相关试题

