搜索
【题目】解方程：x2-3x+2=0
参考答案：
【答案】解答: ∵x2-3x+2=0 ∴（x-1）（x-2）=0，
∴x-1=0或x-2=0，
∴x1=1，x2=2．
【解析】把方程的左边利用十字相乘法因式分解为（x-1）（x-2），再利用积为0的特点求解即可
【考点精析】根据题目的已知条件，利用因式分解法的相关知识可以得到问题的答案，需要掌握已知未知先分离，因式分解是其次．调整系数等互反，和差积套恒等式．完全平方等常数，间接配方显优势．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算正确的是（ ）
A.（﹣a3）2＝﹣a6B.a2a3＝a6C.a8÷a2＝a4D.3a2﹣2a2＝a2
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是( )
A.四个内角对应相等的两个四边形一定相似
B.四条边对应成比例的两个四边形一定相似
C.一个顶角对应相等的两个等腰三角形相似
D.两条边对应成比例且有一个内角相等的两个三角形相似
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了参加中考体育测试，甲，乙，丙三位同学进行足球传球训练，球从一个人脚下随机传到另一个人脚下，且每位传球人传球给其余两人的机会是均等的，由甲开始传球，共传三次．
(l)求请用树状图列举出三次传球的所有可能情况：
(2)传球三次后，球回到甲脚下的概率；
(3)三次传球后，球回到甲脚下的概率大还是传到乙脚下的概率大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D，F在线段AB上，点E，G分别在线段BC和AC上，CD∥EF，∠1=∠2．
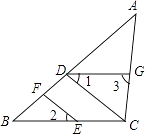
（1）判断DG与BC的位置关系，并说明理由；
（2）若DG是∠ADC的平分线，∠3=85°，且∠DCE：∠DCG=9：10，试说明AB与CD有怎样的位置关系？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数的图象与x轴、y轴分别相交于A、B两点，且与反比例函数y=
（k≠o）的图象在第一象限交于点C，如果点B的坐标为(0，2)．OA=OB，B是线段AC的中点．(l)求点A的坐标及一次函数解析式；
(2)求点C的坐标及反比例函数的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解
如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．
小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
探究发现
△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？ （填“是”或“不是”）．
小丽经过三次折叠发现了∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．
应用提升
（3）小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．
请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．
相关试题
