【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=-![]() x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x+6经过A、C两点.
x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x+6经过A、C两点.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,过点P作PQ∥AC,PQ交直线BC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,作点P关于直线AC的对称点点K,连接QK,当点K落在直线y=-![]() x上时,求线段QK的长.
x上时,求线段QK的长.



参考答案:
【答案】(1) y=-![]() x2-x+6;(2)m=
x2-x+6;(2)m=![]() t2+
t2+![]() t;(3)
t;(3)![]() .
.
【解析】试题分析:(1)先根据一次函数求出A,C点坐标,然后把A,C代入二次函数解析式解方程组即可求出二次函数解析式,(2)根据PQ∥AC,求可得PQ所在直线解析式中的k,根据P点坐标可表示PQ的直线解析式,然后再联立PQ和BC即可求解,(3)先根据点P关于直线AC的对称点K,根据中点坐标公式表示出点K,然后代入直线y=-![]() x,可求出点K,然后根据两点间距离公式可求解QK.
x,可求出点K,然后根据两点间距离公式可求解QK.
试题解析:(1) 因为直线y=x+6经过A,C两点,
所以A(-6,0),C(0,6),
因为抛物线y=![]() x2+bx+c经过A,C两点,把A(-6,0),C(0,6)代入可得:
x2+bx+c经过A,C两点,把A(-6,0),C(0,6)代入可得:
 ,
,
解得: ![]() ,
,
所以二次函数解析式为: ![]() ,
,
(2)因为P点在抛物线上,所以P点坐标是(t, ![]() ),Q点在直线BC上,
),Q点在直线BC上,
设直线BC的解析式为y=kx+b,根据题意可得:
![]() ,解得:
,解得: ![]() ,
,
所以直线BC的解析式为: y=-2x+6,
因为PQ∥AC,
所以可得为: ![]() 解得:
解得: ![]() ,
,
所以直线PQ的直线解析式为: y=x+![]() ,
,
将直线PQ和直线BC联立可求得Q的横坐标:
-2x+6= x+![]() ,
,
-3x=![]() ,
,
x= ![]() ,
,
所以m= ![]() ,
,
(3)根据题意可得:直线QK于直线AC垂直,可得:
![]() ,解得:
,解得: ![]()
所以直线QK的解析式为: y=-x+![]() ,
,
联立直线QK和直线AC,可求得两直线的交点横坐标:
-x+![]() = x+6,
= x+6,
解得: x=![]() ,
,
所以交点纵坐标为: y=![]() ,
,
根据中点坐标公式可得K的坐标为(![]() ,
,![]() ),
),
因为K在y=-![]() x上,
x上,
所以![]() ,解得:
,解得:
因为Q的坐标为(![]() ,
,![]() ), K的坐标为(
), K的坐标为(![]() ,
,![]() ),
),
根据两点之间距离公式可得:
QK=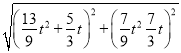 =
=![]() .
.
点睛:本题主要考查二次函数图象性质,一次函数图像性质,解决本题的关键是能够用待定系数法求出一次函数解析式,并联立二次函数解析式求函数的交点是解决本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对应命题“若
 ,则
,则 ”,下面四组
”,下面四组 ,
,  的值中,能说明这个命题是假命题的是( ).
的值中,能说明这个命题是假命题的是( ).A.
 ,
,  B.
B.  ,
,  C.
C.  ,
,  D.
D.  ,
, 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是
 ,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.(
 )画一个三角形,使它的三边长都是有理数.
)画一个三角形,使它的三边长都是有理数.(
 )画一个直角三角形,使它们的三边长都是无理数.
)画一个直角三角形,使它们的三边长都是无理数.(
 )画出与
)画出与 成轴对称且与
成轴对称且与 有公共点的格点三角形(画出一个即可).
有公共点的格点三角形(画出一个即可).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△
 中,
中, ,
, ,点
,点 是
是 上一点,且
上一点,且 ,点
,点 在边
在边 的延长线上,
的延长线上, 平分
平分 ,说明
,说明 ∥
∥ 的理由.
的理由.
解:因为点
 在边
在边 的延长线上(已知),
的延长线上(已知),所以
 (______________________).
(______________________).因为
 (已知),
(已知),所以
 (等式性质).
(等式性质).因为
 平分
平分 (已知),
(已知),所以
 (___________________).
(___________________).因为
 (_________________________________),
(_________________________________),所以
 (等量代换).
(等量代换).所以
 ∥
∥ (____________________________________).
(____________________________________). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62
D. 某次抽奖活动中,中奖的概率为
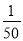 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ∥
∥ ,
, ,
, ,求
,求 的度数.
的度数. 
解:因为
 ∥
∥ (已知),
(已知),所以
 (__________________________).
(__________________________). 因为
 (____________________________),
(____________________________),所以
 (等量代换).
(等量代换).(余下说理过程请写在下方)
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图,
 ∥
∥ ,
, ,
, ,求
,求 的度数.
的度数.小明的思路是过点
 作
作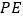 ∥
∥ ,通过平行线的性质来求
,通过平行线的性质来求 .
.
(1)按照小明的思路,求
 的度数;
的度数;(2)问题迁移:如图,
 ∥
∥ ,点
,点 在射线
在射线 上运动,记
上运动,记 ,
, ,当点
,当点 在
在 、
、 两点之间运动时,问
两点之间运动时,问 与
与 、
、 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点
 不在
不在 、
、 两点之间运动时(点
两点之间运动时(点 与点
与点 、
、 、
、 三点不重合),请直接写出
三点不重合),请直接写出 与
与 、
、 之间的数量关系.
之间的数量关系.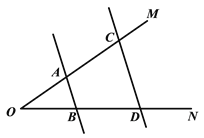
相关试题

