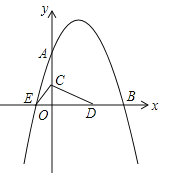
【题目】如图,已知抛物线![]() 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,当t=5时,S最大=
,当t=5时,S最大=![]() ;(3)存在,P(
;(3)存在,P(![]() ,
,![]() )或P(8,0)或P(
)或P(8,0)或P(![]() ,
,![]() ).
).
【解析】
试题分析:(1)将点A、B代入抛物线即可求出抛物线的解析式;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,然后由点A(0,8)、B(8,0),可得OA=8,OB=8,从而可得OD=8﹣t,然后令y=0,求出点E的坐标为(﹣2,0),进而可得OE=2,DE=2+8﹣t=10﹣t,然后利用三角形的面积公式即可求△CED的面积S与D点运动时间t的函数解析式为:![]() ,然后转化为顶点式即可求出最值为:S最大=
,然后转化为顶点式即可求出最值为:S最大=![]() ;
;
(3)由(2)知:当t=5时,S最大=![]() ,进而可知:当t=5时,OC=5,OD=3,进而可得CD=
,进而可知:当t=5时,OC=5,OD=3,进而可得CD=![]() ,从而确定C,D的坐标,即可求出直线CD的解析式,然后过E点作EF∥CD,交抛物线与点P,然后求出直线EF的解析式,与抛物线联立方程组解得即可得到其中的一个点P的坐标,然后利用面积法求出点E到CD的距离,过点D作DN⊥CD,垂足为N,且使DN等于点E到CD的距离,然后求出N的坐标,再过点N作NH∥CD,与抛物线交与点P,然后求出直线NH的解析式,与抛物线联立方程组求解即可得到其中的另两个点P的坐标.
,从而确定C,D的坐标,即可求出直线CD的解析式,然后过E点作EF∥CD,交抛物线与点P,然后求出直线EF的解析式,与抛物线联立方程组解得即可得到其中的一个点P的坐标,然后利用面积法求出点E到CD的距离,过点D作DN⊥CD,垂足为N,且使DN等于点E到CD的距离,然后求出N的坐标,再过点N作NH∥CD,与抛物线交与点P,然后求出直线NH的解析式,与抛物线联立方程组求解即可得到其中的另两个点P的坐标.
试题解析:(1)将点A(0,8)、B(8,0)代入抛物线y=﹣![]() x2+bx+c得:
x2+bx+c得: ,解得:b=3,c=8,∴抛物线的解析式为:
,解得:b=3,c=8,∴抛物线的解析式为:![]() ,故答案为:
,故答案为:![]() ;
;
(2)∵点A(0,8)、B(8,0),∴OA=8,OB=8,令y=0,得:![]() ,解得:
,解得:![]() ,
,![]() ,∵点E在x轴的负半轴上,∴点E(﹣2,0),∴OE=2,根据题意得:当D点运动t秒时,BD=t,OC=t,∴OD=8﹣t,∴DE=OE+OD=10﹣t,∴S=
,∵点E在x轴的负半轴上,∴点E(﹣2,0),∴OE=2,根据题意得:当D点运动t秒时,BD=t,OC=t,∴OD=8﹣t,∴DE=OE+OD=10﹣t,∴S=![]() DEOC=
DEOC=![]() (10﹣t)t=
(10﹣t)t=![]() ,即
,即![]() =
=![]() ,∴当t=5时,S最大=
,∴当t=5时,S最大=![]() ;
;
(3)由(2)知:当t=5时,S最大=![]() ,∴当t=5时,OC=5,OD=3,∴C(0,5),D(3,0),由勾股定理得:CD=
,∴当t=5时,OC=5,OD=3,∴C(0,5),D(3,0),由勾股定理得:CD=![]() ,设直线CD的解析式为:
,设直线CD的解析式为:![]() ,将C(0,5),D(3,0),代入上式得:k=
,将C(0,5),D(3,0),代入上式得:k=![]() ,b=5,∴直线CD的解析式为:
,b=5,∴直线CD的解析式为:![]() ,过E点作EF∥CD,交抛物线与点P,如图1,
,过E点作EF∥CD,交抛物线与点P,如图1,

设直线EF的解析式为:![]() ,将E(﹣2,0)代入得:b=
,将E(﹣2,0)代入得:b=![]() ,∴直线EF的解析式为:
,∴直线EF的解析式为:![]() ,将
,将![]() ,与
,与![]() 联立成方程组得:
联立成方程组得: ,解得:
,解得:![]() ,或
,或 ,∴P(
,∴P(![]() ,
,![]() );
);
过点E作EG⊥CD,垂足为G,∵当t=5时,S△ECD=![]() CDEG=
CDEG=![]() ,∴EG=
,∴EG=![]() ,过点D作DN⊥CD,垂足为N,且使DN=
,过点D作DN⊥CD,垂足为N,且使DN=![]() ,过点N作NM⊥x轴,垂足为M,如图2,
,过点N作NM⊥x轴,垂足为M,如图2,
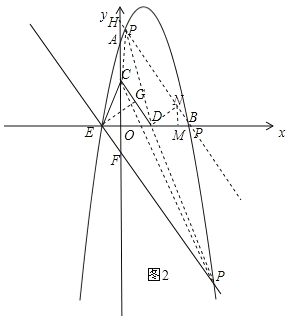
可得△EGD∽△DMN,∴![]() ,∴EGDN=EDDM,即:DM=
,∴EGDN=EDDM,即:DM=![]() =
=![]() ,∴OM=
,∴OM=![]() ,由勾股定理得:MN=
,由勾股定理得:MN=![]() =
=![]() ,∴N(
,∴N(![]() ,
,![]() ),过点N作NH∥CD,与抛物线交与点P,如图2,设直线NH的解析式为:
),过点N作NH∥CD,与抛物线交与点P,如图2,设直线NH的解析式为:![]() ,将N(
,将N(![]() ,
,![]() ),代入上式得:b=
),代入上式得:b=![]() ,∴直线NH的解析式为:
,∴直线NH的解析式为:![]() ,将
,将![]() ,与
,与![]() 联立成方程组得:
联立成方程组得: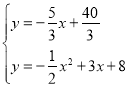 ,解得:
,解得:![]() ,或
,或 ,∴P(8,0)或P(
,∴P(8,0)或P(![]() ,
,![]() ),
),
综上所述:当△CED的面积最大时,在抛物线上存在点P(点E除外),使△PCD的面积等于△CED的最大面积,点P的坐标为:P(![]() ,
,![]() )或P(8,0)或P(
)或P(8,0)或P(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.﹣2x2y3xy2=﹣6x2y2
B.(﹣x﹣2y)(x+2y)=x2﹣4y2
C.6x3y2÷2x2y=3xy
D.(4x3y2)2=16x9y4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形ABCD中,M为AB的中点,N为AD上的一点,且AN=
 AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角)
AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角) 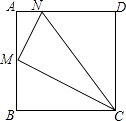
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知抛物线
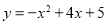 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,
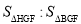 =5:6?
=5:6?(3)图2所示的抛物线是由
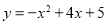 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.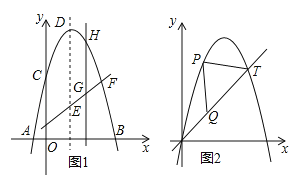
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年我国约有9400000人参加高考,将9400000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线CD∥OA,点E、点F是OA上的动点,CE平分∠OCF,且满足∠FCA=∠FAC.

(1)若∠O=∠ADC,判断AD与OB的位置关系,证明你的结论.
(2)若∠O=∠ADC=60°,求∠ACE的度数.
(3)在(2)的条件下左右平行移动AD,∠OEC和∠CAD存在怎样的数量关系?请直接写出结果(不需写证明过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;

(1)①过点C画OB的平行线CD;②过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到的距离,线段的长度是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是(用“<”号连接).
相关试题

