【题目】在![]() 中,
中,![]() .
.

(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
参考答案:
【答案】(1)见解析(2)见解析
【解析】
(1)连接![]() ,可证得
,可证得![]() ,结合平行线的性质和圆的特性可求得
,结合平行线的性质和圆的特性可求得![]() ,可得出结论;
,可得出结论;
(2)由(1)可知切点是![]() 的角平分线和
的角平分线和![]() 的交点,圆心在
的交点,圆心在![]() 的垂直平分线上,由此即可作出
的垂直平分线上,由此即可作出![]() .
.
(1)证明:如图①,连接![]() ,
,
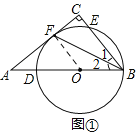
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)如图②所示![]() 为所求.①
为所求.①
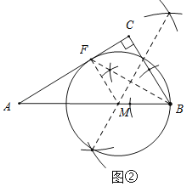
①作![]() 平分线交
平分线交![]() 于
于![]() 点,
点,
②作![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,以
,以![]() 为半径作圆,
为半径作圆,
即![]() 为所求.
为所求.
证明:∵![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
∴![]() ,
,
∴![]() ,
,
又∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 与边
与边![]() 相切.
相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2﹣2+(
 )0+(﹣0.2)2014×52014
)0+(﹣0.2)2014×52014(2)(2a3b)3(﹣8ab2)÷(﹣4a4b3)
(3)(2a+1)2﹣(2a+1)(﹣1+2a)
(4)20192﹣2018×2020(运用整式乘法公式进行计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.

(1)求抛物线的函数表达式;
(2)若点D是y轴上的一点,且以B,C,D为顶点的三角形与△ABC相似,求点D的坐标;
(3)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积;
(4)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 的图象经过点(﹣3,2).
的图象经过点(﹣3,2).(1)求它的解析式;
(2)在直角坐标中画出该反比例函数的图象;
(3)若﹣3<x<﹣2,求y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形
 中,
中, 是
是 的中点,以点
的中点,以点 为直角顶点的直角三角形
为直角顶点的直角三角形 的两边EF、EG分别过点B、C.
的两边EF、EG分别过点B、C.

(1)求证:
 ;
;(2)将
 绕点
绕点 按顺时针方向旋转,当旋转到
按顺时针方向旋转,当旋转到 与
与 重合时停止转动,若
重合时停止转动,若 分别与
分别与 相交于点
相交于点 (如图2).若
(如图2).若 ,求
,求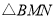 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶,设慢车行驶的时间x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象回答:
(1)甲、乙两地之间的距离为 ;
(2)两车同时出发后 h相遇;
(3)慢车的速度为 千米/小时;快车的速度为 千米/小时;
(4)线段CD表示的实际意义是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a>0)的图象经过点A(1,2).
(1)当b=1,c=﹣4时,求该二次函数的表达式;
(2)已知点M(t﹣1,5),N(t+1,5)在该二次函数的图象上,请直接写出t的取值范围;
(3)当a=1时,若该二次函数的图象与直线y=3x﹣1交于点P,Q,将此抛物线在直线PQ下方的部分图象记为C,
①试判断此抛物线的顶点是否一定在图象C上?若是,请证明;若不是,请举反例;
②已知点P关于抛物线对称轴的对称点为P′,若P′在图象C上,求b的取值范围.
相关试题

