【题目】已知顶点为A(2,一1)的抛物线与y轴交于点B,与x轴交于C、D两点,点C坐标(1,O);
(1)求这条抛物线的表达式;
(2)连接AB、BD、DA,求cos∠ABD的大小;
(3)点P在x轴正半轴上位于点D的右侧,如果∠APB=45°,求点P的坐标.
参考答案:
【答案】(1)y=x2﹣4x+3;(2)![]() ;(3)P(3+
;(3)P(3+![]() ,0)
,0)
【解析】试题分析:(1)由题意得,设抛物线的解析式为y=a(x﹣2)2﹣1,再将C点坐标代入可求a的值;(2)先求证∠BDA=90°,即△ABD是直角三角形,求AB、BD的值,再根据![]() 计算即可;(3)先证明△PDB∽△ADP得出PD2=BDAD,求得PD的值,再根据OP=OD+PD,即可求得点P的坐标;
计算即可;(3)先证明△PDB∽△ADP得出PD2=BDAD,求得PD的值,再根据OP=OD+PD,即可求得点P的坐标;
试题解析:
解:(1)∵顶点为A(2,﹣1)的抛物线经过点C(1,0),
∴可以假设抛物线的解析式为y=a(x﹣2)2﹣1,
把(1,0)代入可得a=1,
∴抛物线的解析式为y=x2﹣4x+3.
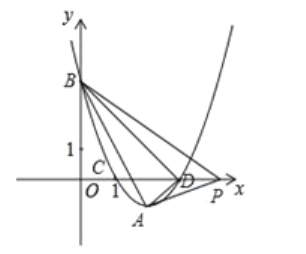
(2)令y=0,x2﹣4x+3=0,解得x=1或3,
∴C(1,0),D(3,0),令x=0,y=3,
∴B(0,3)
∵OB=OD=3,
∴∠BDO=45°,
∵A(2,﹣1),D(3,0),
∴∠ADO=45°,
∴∠BDA=90°,
∵AB=![]() ,BD=
,BD=![]()
∴![]()
(3)∵∠BDO=∠DPB+∠DBP=45°,∠APB=∠DPB+∠DPA=45°,
∴∠DBP=∠APD,
∵∠PDB=∠ADP=135°,
∴△PDB∽△ADP,
∴PD2=BDAD=3![]()
![]() =6,
=6,
∴PD=![]() ,
,
∴OP=3+![]() ,
,
∴点P(3+![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形三边长分别为5cm,8cm,12cm,另一个与它相似的三角形的最长边为4.8cm,求另外两边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2x(x2﹣x+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有四个三角形,分别满足下列条件:①一个角等于另外两个内角之和;②三个内角之比为3:4:5;③三边之比为5:12:13;④三边长分别为5,24,25.其中直角三角形有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,AABC的三个顶点坐标为A(一3,4),B(一4,2),C(一2,1),ΔABC绕原点顺时针旋转90°,得到△A1B1C1,ΔA1B1C1向左平移2个单位,再向下平移5个单位得到△A2B2C2.
(1)画出ΔA1B1Cl和△A2B2C2
(2)P(a,b)是AABC的AC边上一点,ΔABC经旋转、平移后点P的对应点分别为P1、P2,请写出点P1、P2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数有( ) ①已知直角三角形的面积为2,两直角边的比为1:2,则斜边长为
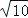 ;
;
②直角三角形的最大边长为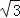 ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为 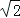 ;
;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x-y)(-y-x)的结果是( )
A. -x2+y2 B. -x2-y2 C. x2-y2 D. x2+y2
相关试题

