【题目】已知如图,在菱形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
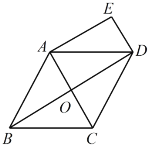
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)见解析;(2)四边形AODE的面积为![]() .
.
【解析】
(1)先判断出四边形AODE是平行四边形,再根据菱形的对角线互相垂直可得AC⊥BD,然后根据有一个角是直角的平行四边形是矩形可得结论;
(2)根据两直线平行,同旁内角互补求出∠ABC=60°,判断出△ABC是等边三角形,然后根据等边三角形的性质求出OA、OB,然后得到OD,再根据矩形的面积公式列式计算即可得解.
解:(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形;
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×6=3,OB=
×6=3,OB=![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=![]() ,
,
∴四边形AODE的面积=OAOD=3×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
,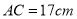 ,
, 边上的高为
边上的高为 ,则
,则 的面积为______
的面积为______ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于
 AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.
AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF.(1)求证:四边形AEDF是菱形;
(2)若BD=6,AF=4,CD=3,求BE的长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,

(1)试说明△ABC与△MED全等;
(2)若∠M=35°,求∠B的度数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直线l上依次摆放着4023个正方形,已知斜放着放置的2011个正方形的面积分别是1、2、3、…、2011,正放置的2012个正方形的面积依次是S1、S2、S3、…S2012,请猜想:S1+S2+S3+S4+…S2012=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,M、N分别是边AD、BC边上的中点,且△ABM≌△DCM;E、F分别是线段BM、CM的中点.
(1)求证:平行四边形ABCD是矩形.
(2)求证:EF与MN互相垂直.

相关试题

