【题目】某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;求x为何值时y的值为1920?
(2)每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
参考答案:
【答案】(1)x=2;(2)每件商品的售价为34元时,商品的利润最大,为1960元
【解析】(1)销售利润=每件商品的利润×(180-10×上涨的钱数),根据每件售价不能高于35元,可得自变量的取值;
(2)利用公式法结合(1)得到的函数解析式可得二次函数的最值,结合实际意义,求得整数解即可;
解:(1)y=(30﹣20+x)(180﹣10x)=﹣10x2+80x+1800(0≤x≤5,且x为整数);
令y=1920得:1920=﹣10x2+80x+1800
x2﹣8x+12=0,
(x﹣2)(x﹣6)=0,
解得x=2或x=6,
∵0≤x≤5,
∴x=2,
(2)由(1)知,y=﹣10x2+80x+1800(0≤x≤5,且x为整数).
∵﹣10<0,
∴当x=![]() =4时,y最大=1960元;
=4时,y最大=1960元;
∴每件商品的售价为34元.
答:每件商品的售价为34元时,商品的利润最大,为1960元;
“点睛”考查二次函数的应用;得到月销售量是解决本题的突破点;注意结合自变量的取值求得相应的售价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则EB的长是( )

A.3 cm
B.4 cm
C.5 cm
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )

A.
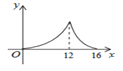 B.
B. 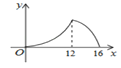 C.
C. 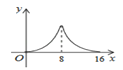 D.
D. 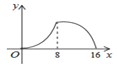
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边 中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为_________

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=45°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1 , O,P2三点构成的三角形是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,BD,CE是角平分线,图中的等腰三角形共有( )

A.6个
B.5个
C.4个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=mx2+2x+1的图像与x轴只有一个公共点,则常数m的值为( )
A.m=1B.m=1或m=2C.m=0D.m=1或m=0
相关试题

