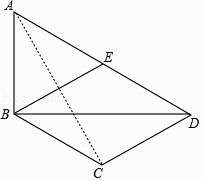
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE. 
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
参考答案:
【答案】
(1)证明:∵AD=2BC,E为AD的中点,
∴DE=BC,
∵AD∥BC,
∴四边形BCDE是平行四边形,
∵∠ABD=90°,AE=DE,
∴BE=DE,
∴四边形BCDE是菱形
(2)解:连接AC.
∵AD∥BC,AC平分∠BAD,
∴∠BAC=∠DAC=∠BCA,
∴AB=BC=1,
∵AD=2BC=2,
∴sin∠ADB= ![]() ,
,
∴∠ADB=30°,
∴∠DAC=30°,∠ADC=60°,
在Rt△ACD中,∵AD=2,
∴CD=1,AC= ![]() .
.
【解析】(1)由DE=BC,DE∥BC,推出四边形BCDE是平行四边形,再证明BE=DE即可解决问题;(2)在Rt△只要证明∠ADC=60°,AD=2即可解决问题;
【考点精析】通过灵活运用直角三角形斜边上的中线,掌握直角三角形斜边上的中线等于斜边的一半即可以解答此题.
-
科目: 来源: 题型:
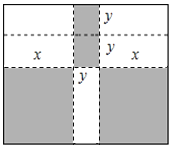
查看答案和解析>>【题目】如图,将一张长方形大铁皮切割成九块,切痕如图虚线所示,其中有两块是边长都为xdm的大正方形,两块是边长都为ydm的小正方形,五块是长宽分别是xdm、ydm的全等小长方形,且x>y.
(1)用含x、y的代数式表示长方形大铁皮的周长为______dm;
(2)若每块小长方形的面积10dm2,四个正方形的面积为58dm2,试求该切痕的总长.
-
科目: 来源: 题型:
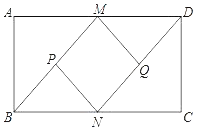
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:BM∥DN;
(2)求证:四边形MPNQ是菱形;
(3)矩形ABCD的边长AB与AD满足什么数量关系时四边形MPNQ为正方形,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2,例如二次三项式x2-2x+9的配方过程如下:x2-2x+9=x2-2x+1-1+9=(x-1)2+8.
请根据阅读材料解决下列问题:
(1)比照上面的例子,将下面的两个二次三项式分别配方:
①x2-4x+1=______;
②3x2+6x-9=3(x2+2x)-9=______;
(2)已知x2+y2-6x+10y+34=0,求3x-2y的值;
(3)已知a2+b2+c2+ab-3b+2c+4=0,求a+b+c的值.
-
科目: 来源: 题型:
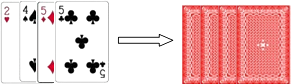
查看答案和解析>>【题目】如图,甲、乙用4张扑克牌玩游戏,他俩将扑克牌洗匀后背面朝上,放置在桌面上,每人抽一张,甲先抽,乙后抽,抽出的牌不放回.甲、乙约定:只有甲抽到的牌面数字比乙大时甲胜;否则乙胜.请你用树状图或列表法说明甲、乙获胜的机会是否相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
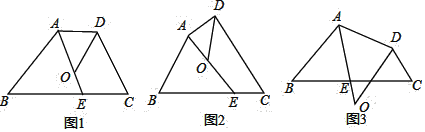
①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE= °;
②如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
相关试题

