【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD. 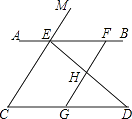
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
参考答案:
【答案】
(1)证明:∵∠CED=∠GHD,
∴CE∥GF;
(2)解:∵CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°
(3)解:∵∠DHG=∠EHF=100°,∠D=30°,
∴∠CGF=100°+30°=130°,
∵CE∥GF,
∴∠C=180°﹣130°=50°,
∵AB∥CD,
∴∠AEC=50°,
∴∠AEM=180°﹣50°=130°
【解析】(1)根据同位角相等两直线平行,可证CE∥GF;(2)根据平行线的性质可得∠C=∠FGD,根据等量关系可得∠FGD=∠EFG,根据内错角相等,两直线平行可得AB∥CD,再根据平行线的性质可得∠AED与∠D之间的数量关系;(3)根据对顶角相等可求∠DHG,根据三角形外角的性质可求∠CGF,根据平行线的性质可得∠C,∠AEC,再根据平角的定义可求∠AEM的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的内角和等于( )
A.90°
B.180°
C.300°
D.360° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边长分别是a,b,c,其中a=3,c=5,且关于x的一元二次方程x2-4x+b=0有两个相等的实数根,判断△ABC的形状.
-
科目: 来源: 题型:
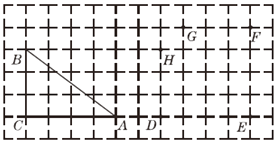
查看答案和解析>>【题目】如图所示,在方格纸中,△ABC的三个顶点及D,E,F,G,H五个点分别位于小正方形的顶点上.
(1)现以D,E,F,G,H中的三个点为顶点画三角形,在所画的三角形中与△ABC不全等但面积相等的三角形是 (只需要填一个三角形);
(2)先从D,E两个点中任意取一个点,再从F,G,H三个点中任意取两个不同的点,以所取的这三个点为顶点画三角形,画树状图求所画三角形与△ABC面积相等的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形的两邻角的角平分线相交所成的角为( ).
A. 锐角 B. 直角 C. 钝角 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红的妈妈买了4筐白菜,以每筐25千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重后的记录分别为+0.25,-1, +0.5, 0.75。小红快速准确地算出了4筐白菜的总质量为( )
A. 一1千克 B. 1千克 C. 99千克 D. 101千克
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3x2+6xy+3y2=_____.
相关试题

