【题目】综合题
(1)已知 ![]() =x,
=x, ![]() =3,z是81的算术平方根,求x﹣y+z的值.
=3,z是81的算术平方根,求x﹣y+z的值.
(2)解不等式组 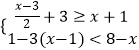 ,并写出该不等式组的整数解.
,并写出该不等式组的整数解.
参考答案:
【答案】
(1)解:∵ ![]() =x,
=x, ![]() =3,z是81的算术平方根,
=3,z是81的算术平方根,
∴x=7,y=27,z=9,
∴x﹣y+z=7﹣27+9=﹣11
(2)解:由 ![]() +3≥x+1得:x≤1,
+3≥x+1得:x≤1,
由1﹣3(x﹣1)<8﹣x得:x>﹣2,
所以﹣2<x≤1,
则不等式组的整数解为﹣1,0,1
【解析】①根据题意,利用立方根即算术平方根定义求出x,y与z的值,可确定出原式的值;
②首先把不等式的解集分别解出,再根据大大取大,小小取小比大的小比小的大取中间,比大的大比小的小无解的原则,求得不等式的解集,再求出其整数解.
【考点精析】掌握一元一次不等式组的解法和一元一次不等式组的整数解是解答本题的根本,需要知道解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 );使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的证明过程,在每步后的横线上填写该步推理的依据. 如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线,求证:DF∥AB
证明:∵BE是∠ABC的角平分线
∴∠1=∠2
又∵∠E=∠1
∴∠E=∠2
∴AE∥BC
∴∠A+∠ABC=180°
又∵∠3+∠ABC=180°
∴∠A=∠3
∴DF∥AB .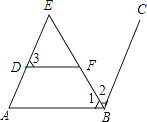
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(1,-2)关于x轴对称的点的坐标是( )
A. (1,-2) B. (-1,2) C. (-1,-2) D. (1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
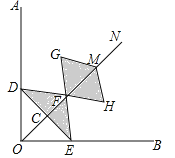
A.
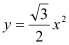 B.
B.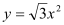 C.
C. D.
D.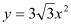
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠1=∠2=50°.
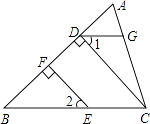
(1)求证:EF∥CD;
(2)若∠AGD=65°,试求∠DCG的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:解不等式(x+2)(x﹣3)>0,根据有理数的乘法法则“两数相乘,同号得正”,可以转化为不等式组求解.
解:(x+2)(x﹣3)>0,转化为①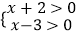 或②
或② 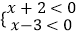 ,解不等式组①,得x>3,解不等式组②,得x<﹣2.
,解不等式组①,得x>3,解不等式组②,得x<﹣2.
∴原不等式(x+2)(x﹣3)>0的解集是x>3或x<﹣2.
请你仿照上面的方法,解下列不等式
(1)(x+7)(2x+8)>0
(2)(3x﹣9)(x+11)<0.
相关试题

