【题目】在Rt△ABC中,∠ACB=90°,点D在边AC上,DE⊥B于点E,连CE.
(1)如图1,已知AC=BC,AD=2CD,
①△ADE与△ABC面积之比;
②求tan∠ECB的值;
(2)如图2,已知 ![]() =
= ![]() =k,求tan∠ECB的值(用含k的代数式表示).
=k,求tan∠ECB的值(用含k的代数式表示).
参考答案:
【答案】
(1)
解:①作EH⊥AD于H,如图1,设CD=x,则AD=2x,AC=BC=3x,
∵AC=BC,∠ACB=90°,
∴△ACB为等腰直角三角形,
∴∠A=45°,
而DE⊥AB,
∴△ADE为等腰直角三角形,
∴AH=HDF=HE=x,
∴S△ADE= ![]() 2xx=x2,
2xx=x2,
∵S△ACB= ![]() 3x3x=
3x3x= ![]() x2,
x2,
∴ ![]() =
= ![]() =
= ![]() ;
;
②在Rt△CHE中,tan∠HEC= ![]() =
= ![]() =2,
=2,
∵HE∥BC,
∴∠BCE=∠HEC,
∴tan∠ECB=2;
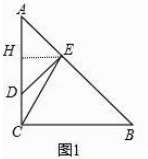
(2)
解:作EH⊥AD于H,如图2,设CD=a,

∵ ![]() =
= ![]() =k,
=k,
∴AD=ak,BC=kAC,
∴AC=(k+1)a,
∴BC=(k2+k)a,
∴AB= ![]() =(k+1)
=(k+1) ![]() a,
a,
∵DE⊥AE,
∴∠AED=90°,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得AE=
,解得AE= ![]() ,
,
∵HE∥BC,
∴△AHE∽△ACB,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= 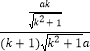 ,
,
∴AH= ![]() ,HE=
,HE= ![]() ,
,
∴CH=AC﹣AH=(k+1)a﹣ ![]() =
= ![]() a,
a,
∴tan∠HEC= ![]() =
= 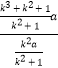 =
= ![]() ,
,
∵HE∥BC,
∴∠BCE=∠HEC,
∴tan∠ECB= ![]() .
.
【解析】(1)①作EH⊥AD于H,如图1,设CD=x,则AD=2x,AC=BC=3x,先证明△ADE为等腰直角三角形得到AH=HDF=HE=x,然后利用三角形面积公式计算出S△ADE和S△ACB , 从而得到 ![]() 的值;②在Rt△CHE中,利用正切的定义得到tan∠HEC=2,再证明∠BCE=∠HEC,所以tan∠ECB=2;(2)作EH⊥AD于H,如图2,设CD=a,则AD=ak,BC=kAC,AC=(k+1)a,BC=(k2+k)a,利用勾股定理定理计算出AB=(k+1)
的值;②在Rt△CHE中,利用正切的定义得到tan∠HEC=2,再证明∠BCE=∠HEC,所以tan∠ECB=2;(2)作EH⊥AD于H,如图2,设CD=a,则AD=ak,BC=kAC,AC=(k+1)a,BC=(k2+k)a,利用勾股定理定理计算出AB=(k+1) ![]() a,再证明△ADE∽△ABC,利用相似比得到AE=
a,再证明△ADE∽△ABC,利用相似比得到AE= ![]() ,接着证明△AHE∽△ACB,利用相似比可得到AH=
,接着证明△AHE∽△ACB,利用相似比可得到AH= ![]() ,HE=
,HE= ![]() ,则CH=
,则CH= ![]() a,则根据正切定义得到tan∠HEC=
a,则根据正切定义得到tan∠HEC= ![]() =
= ![]() ,然后证明∠BCE=∠HEC,从而得到tan∠ECB的值.
,然后证明∠BCE=∠HEC,从而得到tan∠ECB的值.
【考点精析】本题主要考查了相似三角形的性质和相似三角形的应用的相关知识点,需要掌握对应角相等,对应边成比例的两个三角形叫做相似三角形;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图从一个建筑物的A处测得对面楼BC的顶部B的仰角为37°,底部C的俯角为45°,观察点与楼的水平距离AD为40m,求楼BC的高度(参考数据:sin37°≈0.60;cos37°≈0.80;tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线交于点D、E、F,且BF=BC,⊙O是△BEF的外接圆,连接BD.

(1)求证:BD是⊙O的切线;
(2)求证:DEAC=BECE. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于平面直角坐标系中的任意直线MN及点P,取直线MN上一点Q,线段PQ与直线MN成30°角的长度称为点P到直线MN的30°角的距离,记作d(P→MN).
已知O为坐标原点,A(4,0),B(3,3)是平面直角坐标系中两点.根据上述定义,解答下列问题:
(1)点A到直线OB的30°角的距离d(A→OB)=;
(2)已知点G到线段OB的30°角的距离d(G→OB)=2,且点G的横坐标为1,则点G的纵坐标为 .
(3)若点A到直线l:y=kx+1的30°角的距离d(A→l)=4,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=﹣x2+bx+3与x轴交于点A(1,0)和点B,与y轴交于点C.

(1)求抛物线的解析式.
(2)直线y=kx+3k经过点B,与y轴的负半轴交于点D,点P为第二象限内抛物线上一点,连接PD,射线PD绕点P顺时针旋转与线段BD交于点E,且∠EPD=2∠PDC,∠EPD的平分线交线段BD于点H,∠BEP+∠BDP=90°
①若四边形PHDC是平行四边形,求点P的坐标;
②过点E作EF⊥PD,交PD于点G,交y轴于点F,已知PF=3 ,求直线PF的解析式.
,求直线PF的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣
 ,3),反比例函数y=
,3),反比例函数y=  的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( ) 
A.4
B.﹣4
C.2
D.﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )

A.
B.
C.
D.
相关试题

