Question

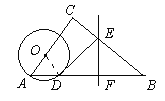
【题目】如图在△ABC中，∠C=90°，点O在AC上，以AO为半径的⊙O交AB于D， BD的垂直平分线交BD于F，交BC于E，连接DE．

（1）求证：DE是⊙O的切线；

（2）若∠B=30°，BC=，且AD∶DF=1∶2，求⊙O的直径．

Answer 1

【答案】（1）证明见解析（2）

【解析】试题分析：（1）直线DE与圆O相切，理由如下：连接OD，由OD=OA，利用等边对等角得到一对角相等，等量代换得到∠ODE为直角，即可得证；

（2）易得△OAD是等边三角形，在Rt△ABC中，由勾股定理可得AC=4，AB=8，设AD=m，则DF=BF=2m，由AB=8得m=,从而可得结果.

试题解析：(1)证明：连OD．

∵OD=OA，∴∠OAD=∠ODA

∵EF垂直平分DB，∴ED=EB，∴∠EDB=∠EBD

又∵∠A＋∠B=90°，∴∠ODA＋∠EDB=90°

∴∠ODE=90°，即OD⊥DE

∵点D在⊙O上， ∴DE是⊙O的切线．

(2)解：∵∠B=30°，∴∠ A=60°，∴△OAD是等边三角形

在Rt△ABC中：设AC=x，则AB=2x，由勾股定理，得

解得，x=4，∴AC=4，AB=8

设AD=m，则DF=BF=2m

由AB=AD＋2DF=m＋4m=8，得m=

∴⊙O的直径=2AD=．