搜索
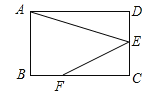
【题目】如图，在矩形ABCD中，点E是CD的中点，点F是BC上一点，且FC=2BF，连接AE，EF．若AB=2，AD=3，则cos∠AEF的值是 ．
参考答案：
【答案】
．
【解析】
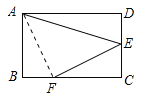
试题分析：连接AF，如图所示：
∵四边形ABCD是矩形，∴∠B=∠C=90°，CD=AB=2，BC=AD=3，∵FC=2BF，∴BF=1，FC=2，∴AB=FC，∵E是CD的中点，∴CE=
CD=1，∴BF=CE，在△ABF和△FCE中，∵AB=FC，∠B=∠C，BF=CE，∴△ABF≌△FCE（SAS），∴∠BAF=∠CFE，AF=FE，∵∠BAF+∠AFB=90°，∴∠CFE+∠AFB=90°，∴∠AFE=180°﹣90°=90°，∴△AEF是等腰直角三角形，∴∠AEF=45°，∴ocs∠AEF=；故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为方便市民出行，减轻城市中心交通压力，佛山市掀起新一轮城市基础设施建设高潮，动工修建贯穿东西、南北的地铁2、3号线，已知修建地铁2号线32千米和3号线66千米共投资581.6亿元；且3号线每千米的平均造价比2号线每千米的平均造价多0.2亿元．
（1）求2号线、3号线每千米的平均造价分别是多少亿元？
（2）除地铁1、2、3号线外，佛山市政府规划未来五年，还要再建108千米的地铁线网．据预算，这168千米地铁线网每千米的平均造价是3号线每千米的平均造价的1.2倍，则还需投资多少亿元？ -
科目： 来源： 题型：
查看答案和解析>>【题目】因式分解：
（1）4a2﹣36
（2）2a2b﹣4ab2+2b3 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点P的坐标为(2－a，3a＋6)，且点P到两坐标轴的距离相等，则点P的坐标是( )
A. (3，3) B. (3，－3) C. (6，－6) D. (3，3)或(6，－6)
-
科目： 来源： 题型：
查看答案和解析>>【题目】图（1）是我们常见的“箭头图”，其中隐藏着哪些数学知识呢？下面请你解决以下问题：
（1）观察如图（1）“箭头图”，试探究∠BDC与∠A、∠B、∠C之间大小的关系，并说明理由；
（2）请你直接利用以上结论，回答下列两个问题：
①如图（2），把一块三角板XYZ放置在△ABC上，使其两条直角边XY、XZ恰好经过点B、C．若∠A=50°，求∠ABX+∠ACX
②如图（3），∠ABD，∠ACD的五等分线分别相交于点G1、G2、G3、G4 ， 若∠BDC=135°，∠BG1C=67°，求∠A的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列运算正确的是（ ）
A.a2+a3=a5
B.a2a3=a6
C.a3÷a2=a
D.（a2）3=a8 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，DE∥BA交AC于点E，DF∥CA交AB于点F，已知CD=3．
（1）求AD的长；
（2）求四边形AEDF的周长．（注意：本题中的计算过程和结果均保留根号）
相关试题
