【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( ) 
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a= ![]() 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形
参考答案:
【答案】D
【解析】解:∵抛物线与x轴的交点A、B的横坐标分别为﹣1,3,∴抛物线的对称轴为直线x=1,则﹣ ![]() =1,
=1,
∴2a+b=0,
∴选项A错误;
∴当自变量取1时,对应的函数图象在x轴下方,
∴x=1时,y<0,则a+b+c<0,
∴选项B错误;
∵A点坐标为(﹣1,0),
∴a﹣b+c=0,而b=﹣2a,
∴a+2a+c=0,
∴3a+c=0,
∴选项C错误;
当a= ![]() ,则b=﹣1,c=﹣
,则b=﹣1,c=﹣ ![]() ,对称轴x=1与x轴的交点为E,如图,∴抛物线的解析式为y=
,对称轴x=1与x轴的交点为E,如图,∴抛物线的解析式为y= ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,把x=1代入得y=
,把x=1代入得y= ![]() ﹣1﹣
﹣1﹣ ![]() =﹣2,
=﹣2,
∴D点坐标为(1,﹣2),
∴AE=2,BE=2,DE=2,
∴△ADE和△BDE都为等腰直角三角形,
∴△ADB为等腰直角三角形,
∴选项D正确.
故选D.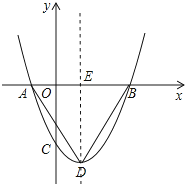
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )
A.
B.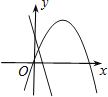
C.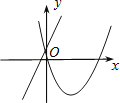
D.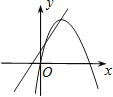
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
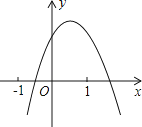
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,则(m﹣1)2+(n﹣1)2的最小值是( )
A.6
B.3
C.﹣3
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b与抛物线y=
 x2交于A(x1 , y1)、B(x2 , y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为 .
x2交于A(x1 , y1)、B(x2 , y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b﹣2c|,Q=|2a﹣b|﹣|3b+2c|,则P,Q的大小关系是 .

相关试题

