搜索
【题目】直线y=kx+b与抛物线y= 
x2交于A（x1 ， y1）、B（x2 ， y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为 ．
参考答案：
【答案】（0，4）
【解析】解：∵直线y=kx+b与抛物线y= 
x2交于A（x1 ， y1）、B（x2 ， y2）两点， ∴kx+b= 
，
化简，得 x2﹣4kx﹣4b=0，
∴x1+x2=4k，x1x2=﹣4b，
又∵OA⊥OB，
∴ 
，
解得，b=4，
即直线y=kx+4，故直线恒过顶点（0，4），
所以答案是：（0，4）．
【考点精析】认真审题，首先需要了解一次函数的性质(一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小)，还要掌握二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a≥2，m2﹣2am+2=0，n2﹣2an+2=0，则（m﹣1）2+（n﹣1）2的最小值是（ ）
A.6
B.3
C.﹣3
D.0 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1和3，则下列结论正确的是（ ）
A.2a﹣b=0
B.a+b+c＞0
C.3a﹣c=0
D.当a=
时，△ABD是等腰直角三角形 -
科目： 来源： 题型：
查看答案和解析>>【题目】某校校园内有一个大正方形花坛，如图甲所示，它由四个边长为3米的小正方形组成，且每个小正方形的种植方案相同．其中的一个小正方形ABCD如图乙所示，DG=1米，AE=AF=x米，在五边形EFBCG区域上种植花卉，则大正方形花坛种植花卉的面积y与x的函数图象大致是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示，且P=|2a+b|+|3b﹣2c|，Q=|2a﹣b|﹣|3b+2c|，则P，Q的大小关系是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的二次函数y=ax2+bx+c的图象经过点（﹣2，y1），（﹣1，y2），（1，0），且y1＜0＜y2 ， 对于以下结论：
①abc＞0；②a+3b+2c≤0；③对于自变量x的任意一个取值，都有
x2+x≥﹣ 
；④在﹣2＜x＜﹣1中存在一个实数x0 ， 使得x0=﹣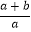 
，
其中结论错误的是 （只填写序号）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，二次函数y=﹣
x2+bx+c的图象与坐标轴交于A、B、C三点，其中点A的坐标为（0，8），点B的坐标为（﹣4，0）．
（1）求该二次函数的表达式及点C的坐标；
（2）点D的坐标为（0，4），点F为该二次函数在第一象限内图象上的动点，连接CD、CF，以CD、CF为邻边作平行四边形CDEF，设平行四边形CDEF的面积为S．
①求S的最大值；
②在点F的运动过程中，当点E落在该二次函数图象上时，请直接写出此时S的值．
相关试题
