【题目】在平面直角坐标系中,点P是第一象限角平分线上的一点,OP=![]() ,直角三角板的直角顶点与点P重合,把直角三角板绕点P转动,另两条直角边所在直线与x轴正半轴、y轴正半轴分别交于A、B两点
,直角三角板的直角顶点与点P重合,把直角三角板绕点P转动,另两条直角边所在直线与x轴正半轴、y轴正半轴分别交于A、B两点

(1)求点P的坐标
(2)若点A的坐标为(0,m),点B的坐标为(n,0),试判断m、n有什么数量关系,并说明理由
(3)连接AB,△ABO的面积是否存在最大值,若存在,求出最大值,若不存在,请说明理由
参考答案:
【答案】(1)(1,1);(2)m+n=2;(3)![]()
【解析】
(1)过P点向坐标轴作垂线PE垂直于x轴PF垂直于y轴,然后利用勾股定理;
(2)证明△PBE≌△PFA,然后直接得出m+n的值;
(3)由(2)可知四边形AOBP的面积是定值,然后根据四边形AOBP的面积=△ABO的面积+△ABP的面积可知当△ABP的面积最小时,△ABO的面积能取到最大值.
解:(1)过P点作过P作PE⊥x轴,PF⊥y轴,

∵P是第一象限角平分线上的一点
∴PE=PF ,∠POE=45°,
∴OE=PE
在Rt△PEO中![]() ,
,
则2=2![]()
∴PE=1
∴P点的坐标为(1,1)
(2)由(1)可知PE⊥x轴,PF⊥y轴
∴PE⊥PF,
∴∠APE+∠APF=90°,
又∵∠APE+∠BPE=90°,
∴∠APF=∠BPE,
∵PE=PF,∠PFA=∠PEB=90°,
∴△APF≌△BPE,
∴AF=BF
则AO+OB=AO+OE+EB=AO+OE+FA=2OE=2
∴m+n=2
(3)△ABO的面积存在最大值为![]() .理由如下:
.理由如下:
由(2)可知△APF≌△BPE,
∴四边形AOBP的面积=四边形OEPF的面积=1,是定值,
又∵四边形AOBP的面积=△ABO的面积+△ABP的面积,
由(2)可知△ABP是等腰直角三角形,面积=![]() ,
,
∴当AP取最小值为1时,△ABP面积有最小值为![]() ,此时△ABO的面积为最大等于
,此时△ABO的面积为最大等于![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是∠AOB的内部任意一点,PM⊥OA,PN⊥OB,垂足分别是M、N,D是OP的中点
(1)求证:DM=DN
(2)连接MN,当∠MPN=______时,△DMN是等边三角形;
(3)探索∠MPN与∠MDN的数量关系,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形ABCD中,AB=6,AD=8,点E为边AD上一点,将△ABE沿BE折叠后得到△BEF.

(1)如图1,若点E为AD的中点,延长BF交边CD于点G.
①求证:DG=FG.
②求FG的长度.
(2)如图2,若点E为边AD的一动点,连接FD,△DEF能否为直角三角形?若能,求出AE的值.若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

-
科目: 来源: 题型:
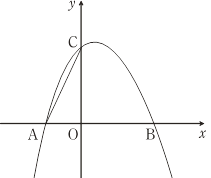
查看答案和解析>>【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0),B(2,0),与y轴相交于点C.
(1)求二次函数的解析式;
(2)若点E是第一象限的抛物线上的一个动点,当四边形ABEC的面积最大时,求点E的坐标,并求出四边形ABEC的最大面积;
(3)若点M在抛物线上,且在y轴的右侧.⊙M与y轴相切,切点为D.以C,D,M为顶点的三角形与△AOC相似,请直接写出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )

A. 10 B. 12 C. 15 D. 18
相关试题

