【题目】在ABCD中,点P和点Q是直线BD上不重合的两个动点,AP∥CQ,AD=BD.
(1)如图①,求证:BP+BQ=BC;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若DQ=1,DP=3,则BC=______.

参考答案:
【答案】(1)证明见解析;(2)图②:BQ﹣BP=BC, 图③:BP﹣BQ=BC;(3)BC=2或4.
【解析】分析:(1)根据平行四边形的性质证明△ADP≌△CBQ,得BQ=PD,由AD=BD=BC得:BC=BD=BP+PD=BP+BQ;(2)图②,证明△ABP≌△CDQ,得PB=DQ,根据线段的和得结论;图③,证明△ADP≌△CBQ,得PD=BQ,同理得出结论;(3)分别代入图①和图②条件下的BC,计算即可.
本题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠ADB=∠CBD,
∵AP∥CQ,∴∠APQ=∠CQB,∴△ADP≌△CBQ, ∴DP=BQ,
∵AD=BD,AD=BC,∴BD=BC,∵BD=BP+DP,∴BC=BP+BQ;
(2)图②:BQ﹣BP=BC,理由是:
∵AP∥CQ,∴∠APB=∠CQD,
∵AB∥CD,∴∠ABD=∠CDB,
∴∠ABP=∠CDQ,∵AB=CD,
∴△ABP≌△CDQ,∴BP=DQ,
∴BC=AD=BD=BQ﹣DQ=BQ﹣BP;
图③:BP﹣BQ=BC,理由是:
同理得:△ADP≌△CBQ,
∴PD=BQ,
∴BC=AD=BD=BP﹣PD=BP﹣BQ;
(3)图①,BC=BP+BQ=DQ+PD=1+3=4,
图②,BC=BQ﹣BP=PD﹣DQ=3﹣1=2,
∴BC=2或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a3﹣16a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b互为相反数,c、d互为倒数,m的绝对值是2,代数式2m+3a+3b+4cd的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2)×3所得结果正确的是( )
A.5
B.6
C.﹣5
D.﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=
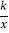 (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为m元,商场按进价提高50%后标价,当销售旺季过后,又以7折(即按标价的70%)的价格开展促销活动,这时这种商品的销售单价为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:①abc;②b2-4ac;③a-b+c;④a+b+c;⑤2a-b;⑥9a-4b中,值小于0的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

