【题目】抛物线y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:①abc;②b2-4ac;③a-b+c;④a+b+c;⑤2a-b;⑥9a-4b中,值小于0的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】根据抛物线的开口方向和对称轴的位置及定顶点的位置,再结合图形可推出a<0,b<0,c<0,由此可判断各式的符号.
解:①由抛物线的开口方向向下可推出a<0;
因为对称轴在y轴左侧,对称轴为x=![]() <0,
<0,
又因为a<0,b<0;
由抛物线与y轴的交点在y轴的负半轴上,
∴c<0,
故abc<0;
②抛物线与x轴有两个交点,b24ac>0;
③当x=1时,ab+c>0;
④当x=1时,y=a+b+c<0;
⑤对称轴x=![]() =1,2a=b,2ab=0;
=1,2a=b,2ab=0;
⑥∵b=2a,且a<0,
∴9a4b=9a8a=a<0,
则①④⑥的值小于0,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点P和点Q是直线BD上不重合的两个动点,AP∥CQ,AD=BD.
(1)如图①,求证:BP+BQ=BC;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若DQ=1,DP=3,则BC=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=
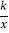 (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为m元,商场按进价提高50%后标价,当销售旺季过后,又以7折(即按标价的70%)的价格开展促销活动,这时这种商品的销售单价为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|x﹣1|+(y+1)2=0,则x2+y2的值是( )
A.0
B.2
C.﹣2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
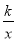 的图象经过点A(-1,
的图象经过点A(-1, 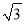 ).
).(1)试确定此反比例函数的解析式;
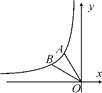
(2)点O是坐标原点,将线段OA绕点O逆时针旋转30°后得到线段OB,求出点B的坐标,并判断点B是否在此反比例函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据某地实验测得的数据表明,高度每增加1km,气温大约下降3℃,已知该地地面温度为21℃.
(1)高空某处高度是6km,求此处的温度是多少;
(2)高空某处温度为﹣24℃,求此处的高度.
相关试题

