搜索
【题目】某学习小组由3名男生和1名女生组成，在一次合作学习后，开始进行成果展示．
（1）如果随机抽取1名同学单独展示，那么女生展示的概率为 ；
（2）如果随机抽取2名同学共同展示，求同为男生的概率．
参考答案：
【答案】（1）
；（2）
.
【解析】
试题（1）4名学生中女生1名，求出所求概率即可；
（2）列表得出所有等可能的情况数，找出同为男生的情况数，即可求出所求概率．
试题解析：（1）如果随机抽取1名同学单独展示，那么女生展示的概率为；
（2）列表如下：
男 | 男 | 男 | 女 | |
男 | ﹣﹣﹣ | （男，男） | （男，男） | （女，男） |
男 | （男，男） | ﹣﹣﹣ | （男，男） | （女，男） |
男 | （男，男） | （男，男） | ﹣﹣﹣ | （女，男） |
女 | （男，女） | （男，女） | （男，女） | ﹣﹣﹣ |
所有等可能的情况有12种，其中同为男生的情况有6种，
则P=
=．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线的方程C1：
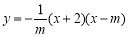（m＞0）与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．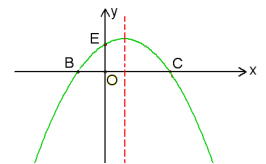
（1）若抛物线C1过点M（2, 2），求实数m的值；
（2）在（1）的条件下，在抛物线的对称轴上找一点H，使得BH＋EH最小，求出点H的坐标；
（3）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】毕业了，九年级
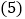班同学组织了一次聚会活动，以纪念他们的友谊．有同学提议去野外聚餐，有同学建议全班一起去看一场电影，也有同学希望开展一次有意义的主题班会．由于资金和时间问题，上面三个提议只能采纳两个，因此同学们决定抽签来决定．全班共有
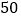名同学轮流抽签，一共有三张签，签上分别标有
、
、
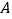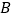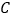三个字母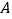．代表野外聚餐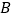，代表看电影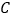，代表开主题班会，每个同学抽两张签后，记下抽取的签然后放回．结束后，将举行抽到次数最多的组合所代表的活动．则这次聚会的活动项目分别是野外聚餐和开展主题班会的概率是（ ）A.
B. 
C. 
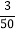D.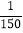 
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个口袋有
个黑球和若干个白球，在不允许将球倒出来的前提下，小明为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，再放回口袋中，…，不断重复上述过程，小明共摸了
次，其中
次摸到黑球．根据上述数据，小明正估计口袋中的白球的个数是________． -
科目： 来源： 题型：
查看答案和解析>>【题目】在一个布袋中装有2个红球和2个篮球，它们除颜色外其他都相同．
（1）搅匀后从中摸出一个球记下颜色，不放回继续再摸第二个球，求两次都摸到红球的概率；
（2）在这4个球中加入x个用一颜色的红球或篮球后，进行如下试验，搅匀后随机摸出1个球记下颜色，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到红球的概率稳定在0.80，请推算加入的是哪种颜色的球以及x的值大约是多少？
-
科目： 来源： 题型：
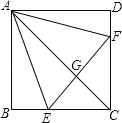
查看答案和解析>>【题目】如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△CEF=2S△ABE．其中正确结论有____．（填序号即可）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．
求证：（1）△AFD≌△CEB．（2）四边形ABCD是平行四边形．
相关试题
