【题目】如图,已知抛物线的方程C1:![]() (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
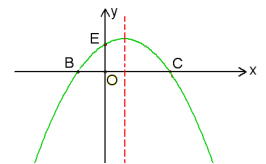
(1)若抛物线C1过点M(2, 2),求实数m的值;
(2)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;
(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
参考答案:
【答案】(1)4;(2)(1,![]() );(3)存在,m=
);(3)存在,m=![]() .
.
【解析】
试题分析:(1)将点(2,2)的坐标代入抛物线解析式,即可求得m的值;(2)根据轴对称以及两点之间线段最短的性质,可知点B、C关于对称轴x=1对称,连接EC与对称轴的交点即为所求的H点,如答图2所示;(3)本问需分两种情况进行讨论:①当△BEC∽△BCF时,如答图3所示.此时可求得m=2![]() +2;②当△BEC∽△FCB时,如答图4所示.此时可以得到矛盾的等式,故此种情形不存在.
+2;②当△BEC∽△FCB时,如答图4所示.此时可以得到矛盾的等式,故此种情形不存在.
试题解析:(1)将M(2,2)代入![]() ,得
,得![]() .解得m=4;
.解得m=4;
(2)如图2,抛物线的对称轴是直线x=1,当H落在线段EC上时,BH+EH最小,设对称轴与x轴的交点为P,那么![]() .因此
.因此![]() .解得
.解得![]() .所以点H的坐标为(1,
.所以点H的坐标为(1,![]() );
);
(3)①如图3,过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.由于∠BCE=∠FBC,所以当![]() ,即
,即![]() 时,△BCE∽△FBC.设点F的坐标为
时,△BCE∽△FBC.设点F的坐标为![]() ,由
,由![]() ,得
,得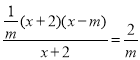 .解得x=m+2.所以F′(m+2, 0).由
.解得x=m+2.所以F′(m+2, 0).由![]() ,得
,得![]() .所以
.所以![]() .由
.由![]() ,得
,得![]() .整理,得0=16.此方程无解.
.整理,得0=16.此方程无解.
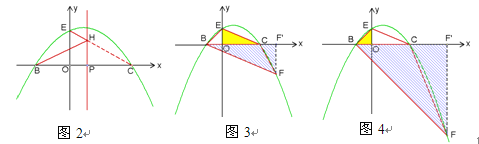
②如图4,作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,由于∠EBC=∠CBF,所以![]() ,即
,即![]() 时,△BCE∽△BFC.在Rt△BFF′中,由FF′=BF′,得
时,△BCE∽△BFC.在Rt△BFF′中,由FF′=BF′,得![]() .解得x=2m.所以F′
.解得x=2m.所以F′![]() .所以BF′=2m+2,
.所以BF′=2m+2,![]() .由
.由![]() ,得
,得![]() .解得
.解得![]() .综合①、②,符合题意的m=
.综合①、②,符合题意的m=![]() .
.
-
科目: 来源: 题型:
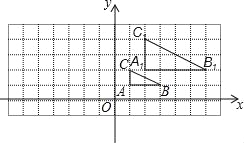
查看答案和解析>>【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
(1)△A1B1C1与△ABC的位似比是 ;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.

(1)求证:△CAE∽△CBF
(2)若BE=1,AE=2,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,M、N分别是CD、BC的中点, 且AM⊥CD,AN⊥BC,已知∠MAN=74°,∠DBC=41°,则∠ADB度数为( ).
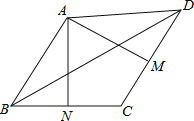
A.15°B.17°
C.16°D.32°
-
科目: 来源: 题型:
查看答案和解析>>【题目】毕业了,九年级
 班同学组织了一次聚会活动,以纪念他们的友谊.有同学提议去野外聚餐,有同学建议全班一起去看一场电影,也有同学希望开展一次有意义的主题班会.由于资金和时间问题,上面三个提议只能采纳两个,因此同学们决定抽签来决定.全班共有
班同学组织了一次聚会活动,以纪念他们的友谊.有同学提议去野外聚餐,有同学建议全班一起去看一场电影,也有同学希望开展一次有意义的主题班会.由于资金和时间问题,上面三个提议只能采纳两个,因此同学们决定抽签来决定.全班共有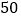 名同学轮流抽签,一共有三张签,签上分别标有
名同学轮流抽签,一共有三张签,签上分别标有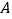 、
、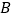 、
、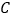 三个字母.
三个字母.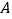 代表野外聚餐,
代表野外聚餐,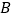 代表看电影,
代表看电影,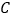 代表开主题班会,每个同学抽两张签后,记下抽取的签然后放回.结束后,将举行抽到次数最多的组合所代表的活动.则这次聚会的活动项目分别是野外聚餐和开展主题班会的概率是( )
代表开主题班会,每个同学抽两张签后,记下抽取的签然后放回.结束后,将举行抽到次数最多的组合所代表的活动.则这次聚会的活动项目分别是野外聚餐和开展主题班会的概率是( )A.
 B.
B.  C.
C. 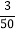 D.
D. 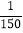
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋有
 个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了
个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了 次,其中
次,其中 次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________.
次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.
相关试题

