搜索
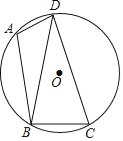
【题目】如图，已知四边形ABCD内接于圆O，连结BD，∠BAD=100°，∠DBC=80°．
（1）求证：BD=CD；
（2）若圆O的半径为9，求
的长（结果保留π）．
参考答案：
【答案】(1)见解析(2) 2π
【解析】分析：（1）直接利用圆内接四边形的对角互补得出∠DCB的度数，再利用∠DCB=∠DBC求出答案；
（2）首先求出
的度数，再利用弧长公式直接求出答案．
详解：（1）∵四边形ABCD内接于圆O，∴∠DCB+∠BAD=180°．
∵∠BAD=100°，∴∠DCB=180°﹣100°=80°．
∵∠DBC=80°，∴∠DCB=∠DBC=80°，∴BD=CD；
（2）∵∠DCB=∠DBC=80°，∴∠BDC=20°，由圆周角定理，得：的度数为：40°，故的长=
=2π．
答：的长为2π．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，函数
与
的图象交于
．（1）求出m、n的值；
（2）直接写出不等式
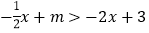的解集；（3）求出
的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
①(－8)＋6-(－13)＋(－6)；
②
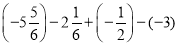
③
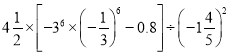
④5(3a2b－ab2+c)－4(2c－ab2＋3a2b)
⑤3x2 －[7x - 2(4x + 2) +2x2]－x2
⑥－14－
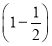÷3×[3－(－3)2]． -
科目： 来源： 题型：
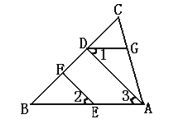
查看答案和解析>>【题目】如图,EF∥AD，∠1=∠2，∠BAC=72 o，求∠AGD的度数.
解：因为EF∥AD
所以∠2= （ ）
又因为∠1=∠2
所以∠1=∠3
所以AB∥ （ ）
所以∠BAC+ =180 o（ ）
因为∠BAC=72 o
所以∠AGD= （ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】我校创造节插花艺术比赛中同学们制作了若干个甲、乙、丙三种造型的花篮．甲种花篮由9朵玫瑰花、16朵水仙花和10朵百合花搭配而成，乙种花篮由6朵玫瑰花、8朵水仙花搭配而成．丙种花篮由6朵玫瑰花、12朵水仙花和10朵百合搭配而成．这些花篮一共用了240朵玫瑰花，300朵百合花，则水仙花一共用了_____朵．
-
科目： 来源： 题型：
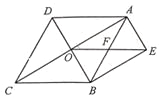
查看答案和解析>>【题目】如图，菱形ABCD的对角线AC、BD相交于点O，BE∥AC，AE∥BD，OE与AB交于点F.
（1）试判断四边形AEBO的形状，并说明理由；
（2）若OE=10，AC=16，求菱形ABCD的面积.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．
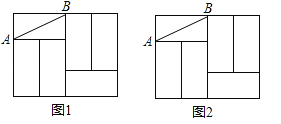
（1）在图1中画出一个45°角，使点A或点B是这个角的顶点，且AB为这个角的一边；
（2）在图2中画出线段AB的垂直平分线．
相关试题
