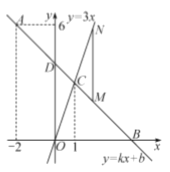
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象经过点
的图象经过点![]() ,且与
,且与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象相交于点
的图象相交于点![]() ,点
,点![]() 的横坐标为1.
的横坐标为1.
(1)求![]() ,
,![]() 的值;
的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)![]() 为射线
为射线![]() 上一点,过
上一点,过![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 点的坐标.
点的坐标.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 点坐标为
点坐标为![]() .
.
【解析】
(1)先确定C点坐标,然后利用待定系数法求一次函数解析式,从而得到k、b的值;
(2)根据函数图象,写出直线y=kx+b在直线y=3x上方所对应的自变量的范围即可;
(3)先确定D点坐标,设点M的横坐标为m,则M(m,m+4),N(m,3m),则4m4=4,然后求出m即可得到M点坐标.
(1)当![]() 时,
时,![]() ,∴
,∴![]() 点坐标为
点坐标为![]() .
.
直线![]() 经过
经过![]() 和
和![]() ,
,
则![]() ,解得:
,解得:![]() .
.
(2)不等式![]() 即
即![]() ,
,
由图象可得解集为:![]() .
.
(3)当![]() 时,
时,![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,∴
,∴![]() .
.
设点![]() 的横坐标为
的横坐标为![]() ,则
,则![]() ,
,![]() ,
,
则![]() ;
;
因为![]() ,∴
,∴![]() ,解得
,解得![]() .
.
即![]() 点坐标为
点坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12千克,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2千克,但耗水量是甲车间的一半.已知A产品售价为30元/千克,水价为5元/吨.设甲车间用x箱原材料生产A产品.
(1)用含x的代数式表示:乙车间用________箱原材料生产A产品;
(2)求两车间生产这批A产品的总耗水量;
(3)若两车间生产这批产品的总耗水为200吨,则该厂如何分配两车间的生产原材料?
(4)用含x的代数式表示这次生产所能获取的利润并化简.(注:利润=产品总售价-购买原材料成本-水费)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.

(1)求证:AE=DC;
(2)已知DC=
 ,求BE的长.
,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的奇数1、3、5、7、9、11……按一定规律排成如下表:
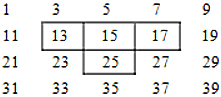
图中的
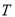 字框框住了四个数,若将
字框框住了四个数,若将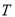 字框上下左右移动,按同样的方式可框住另外的四个数.
字框上下左右移动,按同样的方式可框住另外的四个数.(1)数表中从小到大排列的第9个数是17,第40个数是______,第100个数是______,第
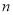 个数是______;
个数是______;(2)设
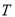 字框内处于中间且靠上方的数是整个数表中从小到大排列的第
字框内处于中间且靠上方的数是整个数表中从小到大排列的第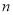 个数,请你用含
个数,请你用含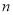 的代数式表示
的代数式表示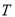 字框中的四个数的和;
字框中的四个数的和;(3)若将
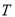 字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由.
字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
-
科目: 来源: 题型:
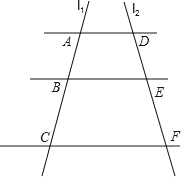
查看答案和解析>>【题目】如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若
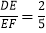 ,AC=14,
,AC=14,(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中,甲,乙两组学生人数都为5人,成绩如下(单位:分):
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数
众数
中位数
甲
______________
8
8
乙
______________
9
______________
(2)已知甲组学生成绩的方差
 ,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定.
,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定.
相关试题

