【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.

(1)求证:AE=DC;
(2)已知DC=![]() ,求BE的长.
,求BE的长.
参考答案:
【答案】(1)证明见试题解析;(2)2.
【解析】
试题(1)由矩形的性质及已知条件可得到△AEF≌△DCE,即可证明AE=DC;
(2)由(1)得到AE=DC,在Rt△ABE中由勾股定理可求得BE的长.
试题解析:(1)在矩形ABCD中,∠A=∠D=90°,∴∠1+∠2=90°,∵EF⊥EC,∴∠FEC=90°,∴∠2+∠3=90°,∴∠1=∠3,在△AEF和△DCE中,∵∠A=∠D,∠1=∠3,EF=EC,∴△AEF≌△DCE(AAS),∴AE=DC;
(2)由(1)得AE=DC,∴AE=DC=![]() ,在矩形ABCD中,AB=CD=
,在矩形ABCD中,AB=CD=![]() ,在R△ABE中,
,在R△ABE中,![]() ,即
,即![]() ,∴BE=2.
,∴BE=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里有
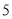 个除颜色外都相同的球,其中有
个除颜色外都相同的球,其中有 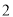 个红球,
个红球, 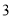 个黄球.
个黄球.(1) 若从中随意摸出一个球,求摸出红球的可能性;
(2) 若要使从中随意摸出一个球是红球的可能性为
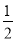 ,求袋子中需再加入几个红球?
,求袋子中需再加入几个红球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
(1)求证:△EDF≌△CBF;
(2)求∠EBC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12千克,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2千克,但耗水量是甲车间的一半.已知A产品售价为30元/千克,水价为5元/吨.设甲车间用x箱原材料生产A产品.
(1)用含x的代数式表示:乙车间用________箱原材料生产A产品;
(2)求两车间生产这批A产品的总耗水量;
(3)若两车间生产这批产品的总耗水为200吨,则该厂如何分配两车间的生产原材料?
(4)用含x的代数式表示这次生产所能获取的利润并化简.(注:利润=产品总售价-购买原材料成本-水费)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的奇数1、3、5、7、9、11……按一定规律排成如下表:
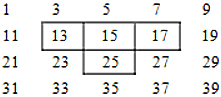
图中的
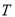 字框框住了四个数,若将
字框框住了四个数,若将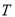 字框上下左右移动,按同样的方式可框住另外的四个数.
字框上下左右移动,按同样的方式可框住另外的四个数.(1)数表中从小到大排列的第9个数是17,第40个数是______,第100个数是______,第
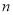 个数是______;
个数是______;(2)设
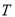 字框内处于中间且靠上方的数是整个数表中从小到大排列的第
字框内处于中间且靠上方的数是整个数表中从小到大排列的第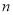 个数,请你用含
个数,请你用含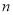 的代数式表示
的代数式表示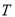 字框中的四个数的和;
字框中的四个数的和;(3)若将
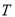 字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由.
字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图象经过点
的图象经过点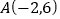 ,且与
,且与 轴相交于点
轴相交于点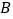 ,与
,与 轴交于点
轴交于点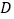 ,与正比例函数
,与正比例函数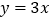 的图象相交于点
的图象相交于点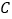 ,点
,点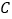 的横坐标为1.
的横坐标为1.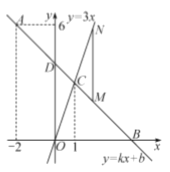
(1)求
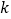 ,
,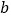 的值;
的值;(2)请直接写出不等式
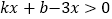 的解集;
的解集;(3)
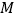 为射线
为射线 上一点,过
上一点,过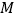 作
作 轴的平行线交
轴的平行线交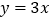 于点
于点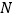 ,当
,当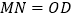 时,求
时,求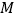 点的坐标.
点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
相关试题

