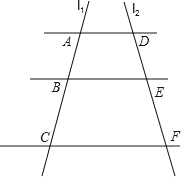
【题目】如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若![]() ,AC=14,
,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
参考答案:
【答案】(1)AB=4;(2)BE=9.
【解析】【详解】(1)根据三条平行线截两条直线,所得的对应线段成比例可得![]() ,从而可得
,从而可得![]() ,再由AC=14即可求出AB的长;
,再由AC=14即可求出AB的长;
(2)过点A作AG∥DF交BE于点H,交CF于点G,运用比例关系求出BH及HE的长,然后即可得出BE的长.
【详解】(1)∵AD∥BE∥CF,
∴![]() ,
,
∴![]() ,
,
∵AC=14,
∴AB=4,
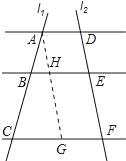
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴![]() ,
,
∴BH=2,
∴BE=2+7=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的奇数1、3、5、7、9、11……按一定规律排成如下表:
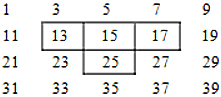
图中的
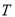 字框框住了四个数,若将
字框框住了四个数,若将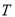 字框上下左右移动,按同样的方式可框住另外的四个数.
字框上下左右移动,按同样的方式可框住另外的四个数.(1)数表中从小到大排列的第9个数是17,第40个数是______,第100个数是______,第
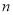 个数是______;
个数是______;(2)设
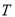 字框内处于中间且靠上方的数是整个数表中从小到大排列的第
字框内处于中间且靠上方的数是整个数表中从小到大排列的第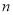 个数,请你用含
个数,请你用含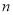 的代数式表示
的代数式表示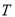 字框中的四个数的和;
字框中的四个数的和;(3)若将
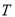 字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由.
字框上下左右移动,框住的四个数的和能等于406吗?如能,求出这四个数,如不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图象经过点
的图象经过点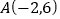 ,且与
,且与 轴相交于点
轴相交于点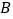 ,与
,与 轴交于点
轴交于点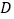 ,与正比例函数
,与正比例函数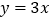 的图象相交于点
的图象相交于点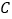 ,点
,点 的横坐标为1.
的横坐标为1.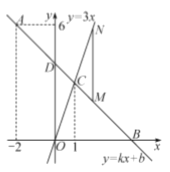
(1)求
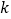 ,
,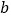 的值;
的值;(2)请直接写出不等式
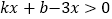 的解集;
的解集;(3)
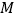 为射线
为射线 上一点,过
上一点,过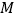 作
作 轴的平行线交
轴的平行线交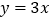 于点
于点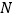 ,当
,当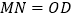 时,求
时,求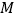 点的坐标.
点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中,甲,乙两组学生人数都为5人,成绩如下(单位:分):
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数
众数
中位数
甲
______________
8
8
乙
______________
9
______________
(2)已知甲组学生成绩的方差
 ,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定.
,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 为直线
为直线 上一点,以
上一点,以 为顶点作
为顶点作 ,射线
,射线 平分
平分
(1)如图①,
 与
与 的数量关系为______
的数量关系为______
(2)如图①,如果
 ,请你求出
,请你求出 的度数并说明理由;
的度数并说明理由;(3)若将图①中的
 绕点
绕点 旋转至图②的位置,
旋转至图②的位置, 依然平分
依然平分 ,若
,若 ,请直接写出
,请直接写出 的度数
的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A地在数轴上表示的数为-16,AB两地相距50个单位长度.小明从A地出发去B地,以每分钟2个单位长度的速度行进,第一次他向左1单位长度,第二次向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度…,按此规律行进.

(1)求出B地在数轴上表示的数;
(2)若B地在原点的右侧,经过第8次行进后小明到达点P,此时点P与点B相距几个单位长度?8次运动完成后一共经过了几分钟?
(3)若经过n次(n为正整数)行进后,小明到达点Q,请你直接写出:点Q在数轴上表示的数应如何表示?
相关试题

