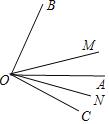
【题目】如图,已知OM、OA、ON是∠BOC内的三条射线,ON平分∠AOC,OM平分∠BOC,且∠AOB+∠MON=120°,则∠MON=______°.
参考答案:
【答案】40
【解析】
设∠AOB=x°,∠MON=y°,先表示出∠BOC的度数,再根据角平分线的定义表示出∠MOC与∠NOC,然后根据∠MON=∠MOC-∠NOC列式整理得出规律,∠MON的度数等于∠AOB的一半,进行求解即可.
解:设∠AOB=x°,∠MON=y°,
则∠BOC=∠AOB+∠AOC=x°+∠AOC,
因为ON平分∠AOC,OM平分∠BOC.
所以∠MOC=![]() ∠BOC=
∠BOC=![]() +
+![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠AOC,
∠AOC,
所以∠MON=∠MOC-∠NOC=![]() x,
x,
即y=![]() x,
x,
由题意可得:x+![]() =120°,
=120°,
解得x=80°,
所以∠MON= y =40°.
故答案为:40
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=
 ∠CGE.其中正确的结论是( )
∠CGE.其中正确的结论是( )
A. ②③B. ①②④C. ①③④D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC=8cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=b,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形并写出你的结论(不必说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的不等式表示下列不等关系:
(1)x减去6大于12;
(2)x的2倍与5的差是负数;
(3)x的3倍与4的和是非负数;
(4)y的5倍与9的差不大于
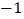 ;
; -
科目: 来源: 题型:
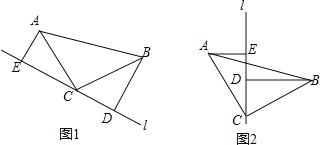
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC,直线l过点C,BD⊥l,AE⊥l,垂足分别为D、E.
(1)当直线l不与底边AB相交时,求证:ED=AE+BD;
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB相交时,请你探究ED、AE、BD三者之间的数量关系.
相关试题

