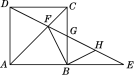
【题目】如图,E为正方形ABCD的边AB的延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点.
求证:FB⊥BH.
参考答案:
【答案】证明见解析
【解析】
根据正方形的性质,用SAS判定△DCF≌△BCF,从而得到对应角相等,再根据中线的性质及角之间的关系便可推出FB⊥BH..
证明:∵四边形ABCD是正方形,
∴CD=CB,∠DCF=∠BCF=45°,
DC∥AE,∠CBE=90°,
∴∠CDF=∠E.
又∵CF=CF,∴△DCF≌△BCF.
∴∠CDF=∠CBF.∴∠CBF=∠E.
∵H为GE的中点,
∴HB=HG=![]() GE.
GE.
∴∠HGB=∠HBG.
∵∠CDG+∠CGD=90°,∠CGD=∠HGB=∠HBG,
∴∠FBG+∠HBG=90°,
即∠FBH=90°,∴FB⊥BH.
-
科目: 来源: 题型:
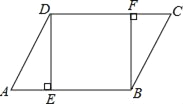
查看答案和解析>>【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.
-
科目: 来源: 题型:
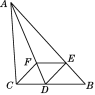
查看答案和解析>>【题目】如图,在△ABC中,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF∥BC交AD于点F.
求证:四边形CDEF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
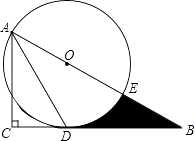
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将矩形ABCD沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,求阴影部分图形的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线相交于点O,点O也是正方形A′B′C′O的一个顶点,如果两个正方形的边长都等于1,那么正方形A′B′C′O绕顶点O转动,两个正方形重叠部分的面积大小有什么规律?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位,再向下平移4个长度单位得到点C.
(1)用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;
(2)若t=1时,平移线段AB,使点A、B到坐标轴上的点
 、
、 处,指出平移的方向和距离,并求出点
处,指出平移的方向和距离,并求出点 、
、 的坐标;
的坐标;(3)若t=0时,平移线段AB至MN(点A与点M对应),使点M落在x轴的负半轴上,三角形MNB的面积为4,试求点M、N的坐标.
相关试题

