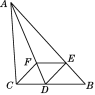
【题目】如图,在△ABC中,∠BAC的平分线交BC于点D,E是AB上一点,且AE=AC,EF∥BC交AD于点F.
求证:四边形CDEF是菱形.
参考答案:
【答案】证明见解析
【解析】
根据AE=AC,得出△ACE为等腰三角形,根据AD是∠BAC的平分线得出AO⊥CE,且OC=OE. 由EF∥CD得出∠OEF=∠OCD,再根据ASA证明△DOC≌△FOE,
得出OD=OF,直接由菱形的判定可知四边形CDEF是菱形.
证明:如图,连接CE,交AD于点O.
∵AC=AE,
∴△ACE为等腰三角形.
∵AO平分∠CAE,
∴AO⊥CE,且OC=OE.
∵EF∥CD,
∴∠OEF=∠OCD.
又∵∠DOC=∠FOE,
∴△DOC≌△FOE(ASA).
∴OD=OF.
即CE与DF互相垂直且平分,
∴四边形CDEF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
类别
时间t(小时)
人数
A
t≤0.5
5
B
0.5<t≤1
20
C
1<t≤1.5
a
D
1.5<t≤2
30
E
t>2
10
请根据图表信息解答下列问题:
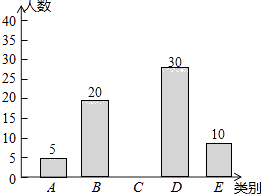
(1)a=;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
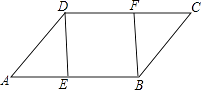
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形. -
科目: 来源: 题型:
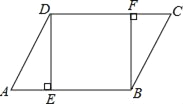
查看答案和解析>>【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
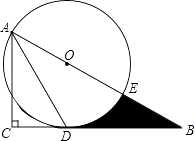
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π) -
科目: 来源: 题型:
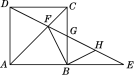
查看答案和解析>>【题目】如图,E为正方形ABCD的边AB的延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点.
求证:FB⊥BH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将矩形ABCD沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,求阴影部分图形的周长.

相关试题

