【题目】如图,正方形ABCD的对角线相交于点O,点O也是正方形A′B′C′O的一个顶点,如果两个正方形的边长都等于1,那么正方形A′B′C′O绕顶点O转动,两个正方形重叠部分的面积大小有什么规律?请说明理由.

参考答案:
【答案】答案见解析
【解析】
先由正方形的性质可得OB=OC,∠EOF=∠BOC,进而求得∠BOE=∠COF,从而可判断△BOE≌△COF,所以S△BOE=S△COF.那么两个正方形重叠部分的面积等于S△BOC.
至此问题即可迎刃而解.
解:两个正方形重叠部分的面积保持不变,始终是![]() .
.
理由如下:
∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°.
∵四边形A′B′C′O是正方形,
∴∠EOF=90°.∴∠EOF=∠BOC.
∴∠EOF-∠BOF=
∠BOC-∠BOF,
即∠BOE=∠COF.
∴△BOE≌△COF.
∴S△BOE=S△COF.
∴两个正方形重叠部分的面积等于S△BOC.
∵S正方形ABCD=1×1=1,
∴S△BOC=![]() S正方形ABCD=
S正方形ABCD=![]() .
.
∴两个正方形重叠部分的面积保持不变,始终是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
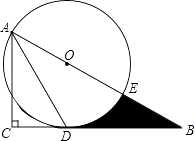
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π) -
科目: 来源: 题型:
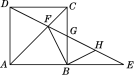
查看答案和解析>>【题目】如图,E为正方形ABCD的边AB的延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点.
求证:FB⊥BH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将矩形ABCD沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,求阴影部分图形的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位,再向下平移4个长度单位得到点C.
(1)用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;
(2)若t=1时,平移线段AB,使点A、B到坐标轴上的点
 、
、 处,指出平移的方向和距离,并求出点
处,指出平移的方向和距离,并求出点 、
、 的坐标;
的坐标;(3)若t=0时,平移线段AB至MN(点A与点M对应),使点M落在x轴的负半轴上,三角形MNB的面积为4,试求点M、N的坐标.
-
科目: 来源: 题型:
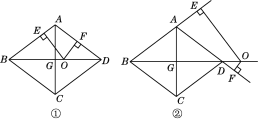
查看答案和解析>>【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
-
科目: 来源: 题型:
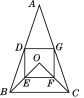
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点O在△ABC的内部,∠BOC=90°,OB=OC,D,E,F,G分别是AB,OB,OC,AC的中点.
(1)求证:四边形DEFG是矩形;
(2)若DE=2,EF=3,求△ABC的面积.
相关试题

