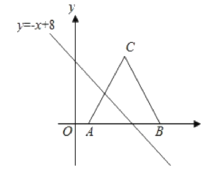
【题目】如图△ABC,AC=BC=13,把△ABC放在平面直角坐标系中,且点A、B的坐标分别为(2,0)、(12,0),将△ABC沿x轴向左平移,当点C落在直线y=-x+8上时,线段AC扫过的面积为_____;
参考答案:
【答案】132
【解析】
过点C作CD⊥x轴于点D,由点A、B的坐标利用勾股定理可求出点C的坐标,再利用一次函数图象上点的坐标特征可求出点C移动后的坐标,借助平行四边形的面积即可得出线段AC扫过的面积.
过点C作CD⊥x轴于点D,如图所示。

∵点A,B的坐标分别为(2,0),(12,0),AC=BC=13,
∴AD=BD=![]() AB=5,
AB=5,
∴CD=![]() .
.
∴点C的坐标为(7,12).
当y=12时,有12=x+8,
解得:x=4,
∴点C平移后的坐标为(4,12).
∴△ABC沿x轴向左平移7(4)=11个单位长度,
∴线段AC扫过的面积S=11CD=132.
故答案为:132
-
科目: 来源: 题型:
查看答案和解析>>【题目】工厂加工某种茶叶,计划一周生产
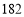 千克,平均每天生产
千克,平均每天生产 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):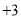 ,
, ,
,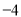 ,
,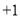 ,
,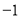 ,
,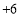 ,
,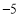 .
.(
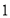 )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?(
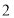 )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克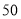 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克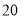 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少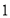 千克扣除
千克扣除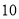 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少? -
科目: 来源: 题型:
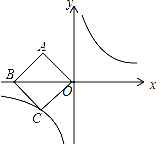
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4
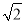 ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1) ∠DCF=
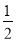 ∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )
∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )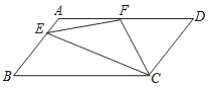
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
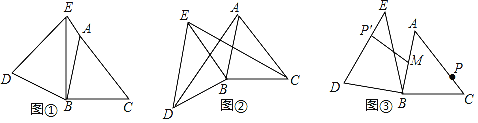
查看答案和解析>>【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△DBE.
(1)当旋转成如图①,点E在线段CA的延长线上时,则∠CED的度数是 度;
(2)当旋转成如图②,连接AD、CE,若△ABD的面积为4,求△CBE的面积;
(3)点M为线段AB的中点,点P是线段AC上一动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点P′,连接MP′,如图③,直接写出线段MP′长度的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+
 a2)+(3b+
a2)+(3b+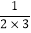 a2)+…+(9b+
a2)+…+(9b+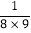 a2)的值.
a2)的值.
相关试题

