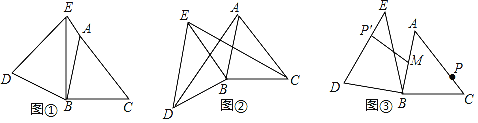
【题目】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△DBE.
(1)当旋转成如图①,点E在线段CA的延长线上时,则∠CED的度数是 度;
(2)当旋转成如图②,连接AD、CE,若△ABD的面积为4,求△CBE的面积;
(3)点M为线段AB的中点,点P是线段AC上一动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点P′,连接MP′,如图③,直接写出线段MP′长度的最大值和最小值.
参考答案:
【答案】(1)90;(2)S△CBE=![]() ;(3)线段MP'的最大值为7,最小值为
;(3)线段MP'的最大值为7,最小值为![]() ﹣2.
﹣2.
【解析】试题分析:(1)根据旋转的性质可知:∠DEC=45°,再由等边对等角得∠BEC=45°,则∠CED=90°;
(2)由△ABC≌△DBE得出BA=BD,BC=BE,进而得出![]() ,证明△ABD∽△CBE,根据面积比等于相似比的平方求出△CBE的面积;
,证明△ABD∽△CBE,根据面积比等于相似比的平方求出△CBE的面积;
(3)作辅助线,当点P在F处时BP最小,则BG最小,MP'最小;当点P在点C处时,BP最大,则BH最大,MP'最大,代入计算即可得出结论.
试题解析:解:(1)由旋转得:∠DEB=∠ACB=45°,BC=BE,∴∠ACB=∠BEC=45°,∴∠CED=90°.故答案为:90;
(2)∵△ABC≌△DBE,∴BA=BD,BC=BE,∠ABC=∠DBE,∴![]() .∵∠ABD=∠CBE,∴△ABD∽△CBE,∴
.∵∠ABD=∠CBE,∴△ABD∽△CBE,∴![]() =(
=(![]() )2=
)2=![]() .∵S△ABD=4,∴S△CBE=
.∵S△ABD=4,∴S△CBE=![]() ;
;
(3)∵M是AB的中点,∴BM=![]() AB=2.如图③,过点B作BF⊥AC,F为垂足.∵△ABC为锐角三角形,∴点F在线段AC上.在Rt△BCF中,BF=BC×sin45°=
AB=2.如图③,过点B作BF⊥AC,F为垂足.∵△ABC为锐角三角形,∴点F在线段AC上.在Rt△BCF中,BF=BC×sin45°=![]() ,以B为圆心,BF为半径画圆交AB于G,BP'有最小值BG,∴MP'的最小值为MG=BG﹣BM=
,以B为圆心,BF为半径画圆交AB于G,BP'有最小值BG,∴MP'的最小值为MG=BG﹣BM=![]() ﹣2,以B为圆心,BC为半径画圆交AB的延长线于H,BP'有最大值BH.此时MP'的最大值为BM+BH=2+5=7,∴线段MP'的最大值为7,最小值为
﹣2,以B为圆心,BC为半径画圆交AB的延长线于H,BP'有最大值BH.此时MP'的最大值为BM+BH=2+5=7,∴线段MP'的最大值为7,最小值为![]() ﹣2.
﹣2.

-
科目: 来源: 题型:
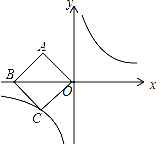
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4
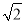 ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1) ∠DCF=
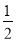 ∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )
∠BCD;(2)EF=CF;(3)S△CDF=S△CEF;(4)∠DFE=3∠AEF.其中正确结论的个数是( )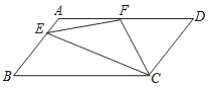
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
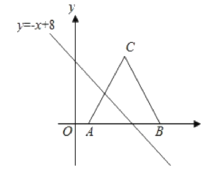
查看答案和解析>>【题目】如图△ABC,AC=BC=13,把△ABC放在平面直角坐标系中,且点A、B的坐标分别为(2,0)、(12,0),将△ABC沿x轴向左平移,当点C落在直线y=-x+8上时,线段AC扫过的面积为_____;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+
 a2)+(3b+
a2)+(3b+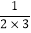 a2)+…+(9b+
a2)+…+(9b+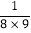 a2)的值.
a2)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)模型建立,如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA;
(2)模型应用:
①已知直线y=
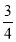 x+3与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线.求直线AC的解析式;
x+3与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线.求直线AC的解析式;②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=2x-6上的一点,若△APD是不以A为直角顶点的等腰直角三角形,请直接写出所有符合条件的点D的坐标.
相关试题

