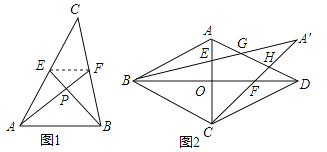
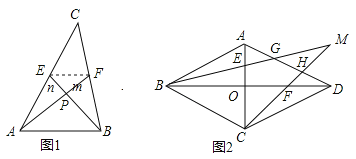
【题目】尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:![]() .
.
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故![]() ,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证.
,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证.
(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)5.
【解析】
试题分析:(1)设PF=m,PE=n,连结EF,如图1,根据三角形中位线性质得EF∥AB,EF=![]() c,则可判断△EFP∽△BPA,利用相似比得到PB=2n,PA=2m,接着根据勾股定理得到
c,则可判断△EFP∽△BPA,利用相似比得到PB=2n,PA=2m,接着根据勾股定理得到![]() ,
,![]() ,则
,则![]() ,而
,而![]() ,所以
,所以![]() ;
;
(2)利用(1)的结论得![]() =
=![]() =45,再利用△AEG∽△CEB可计算出AG=1,同理可得DH=1,则GH=1,然后利用GH∥BC,根据平行线分线段长比例定理得到MB=3GM,MC=3MH,然后等量代换后可得
=45,再利用△AEG∽△CEB可计算出AG=1,同理可得DH=1,则GH=1,然后利用GH∥BC,根据平行线分线段长比例定理得到MB=3GM,MC=3MH,然后等量代换后可得![]() =5.
=5.
试题解析:(1)设PF=m,PE=n,连结EF,如图1,∵AF,BE是△ABC的中线,∴EF为△ABC的中位线,AE=![]() b,BF=
b,BF=![]() a,∴EF∥AB,EF=
a,∴EF∥AB,EF=![]() c,∴△EFP∽△BPA,∴
c,∴△EFP∽△BPA,∴![]() ,即
,即![]() =
=![]() ,∴PB=2n,PA=2m,在Rt△AEP中,∵
,∴PB=2n,PA=2m,在Rt△AEP中,∵![]() ,∴
,∴![]() ①,在Rt△AEP中,∵
①,在Rt△AEP中,∵![]() ,∴
,∴![]() ②,①+②得
②,①+②得![]() ,在Rt△EFP中,∵
,在Rt△EFP中,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
(2)∵四边形ABCD为菱形,∴BD⊥AC,∵E,F分别为线段AO,DO的中点,由(1)的结论得![]() =
=![]() =45,∵AG∥BC,∴△AEG∽△CEB,∴
=45,∵AG∥BC,∴△AEG∽△CEB,∴![]() ,∴AG=1,同理可得DH=1,∴GH=1,∴GH∥BC,∴
,∴AG=1,同理可得DH=1,∴GH=1,∴GH∥BC,∴![]() ,∴MB=3GM,MC=3MH,∴
,∴MB=3GM,MC=3MH,∴![]() ,∴
,∴![]() =5.
=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年元月份利润为500万元,以后两个月均匀增长,第一季度的利润1820万元,设该公司利润月平均增长率为x,根据题意可列方程_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】任意写出一个偶数和一个奇数,两数之和是奇数的概率是 , 两数之和是偶数的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,0),B(3,0),C(0,2),CD∥x轴,CD=AB.
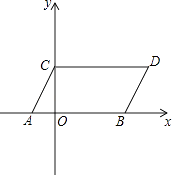
(1)求点D的坐标:
(2)四边形OCDB的面积S四边形OCDB;
(3)在 y轴上是否存在点P,使S△PAB=S四边形OCDB?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
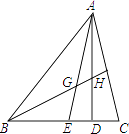
查看答案和解析>>【题目】如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点G,AD与BF相交于点H,∠BAC=50°,∠C=70°,则∠AHB= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣2x2向左平移3个单位长度所得图象的解析式是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F、E分别为AC、AD上两动点,连接CE、EF,则CE+EF的最小值为 .

相关试题

