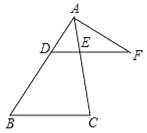
【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )
A.29.1米
B.31.9米
C.45.9米
D.95.9米
参考答案:
【答案】A
【解析】解:作DE⊥AB于E点,作AF⊥DE于F点,如图: ,
,
设DE=xm,CE=2.4xm,由勾股定理,得
x2+(2.4x)2=1952 ,
解得x≈75m,
DE=75m,CE=2.4x=180m,
EB=BC﹣CE=306﹣180=126m.
∵AF∥DG,
∴∠1=∠ADG=20°,
tan∠1=tan∠ADG= ![]() =0.364.
=0.364.
AF=EB=126m,
tan∠1= ![]() =0.364,
=0.364,
DF=0.364AF=0.364×126=45.9,
AB=FE=DE﹣DF=75﹣45.9≈29.1m,
故答案为:A.
根据勾股定理求出DE的值,再根据解直角三角形AF、BE、DF的值,求出AB=FE=DE﹣DF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,菱形
中,菱形 的顶点
的顶点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,点
,点 在第一象限内,对角线
在第一象限内,对角线 与
与 轴平行,直线
轴平行,直线 与
与 轴、
轴、 轴分别交于点
轴分别交于点 .将菱形
.将菱形 沿
沿 轴向左平移
轴向左平移 个单位.当点
个单位.当点 落在
落在 的内部时(不包括三角形的边),则
的内部时(不包括三角形的边),则 的取值范围是__________.
的取值范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据:
 ≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )
≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( ) 
A.7.27
B.16.70
C.17.70
D.18.18 -
科目: 来源: 题型:
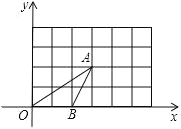
查看答案和解析>>【题目】如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
(1)在图中画出△DEF;
(2)点E是否在直线OA上?为什么?
(3)△OAB与△DEF______位似图形(填“是”或“不是”)
-
科目: 来源: 题型:
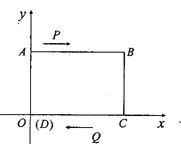
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:

⑴根据如图1,写出一个等式:
⑵如图2,若长方形的长AB为10,AD宽为6,分别求a、b的值;
⑶如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=6,ab=10,请求出阴影部分的面积.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果
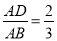 ,DE=6,求边BC的长;
,DE=6,求边BC的长;(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
相关试题

