搜索
【题目】已知，△ABC中，∠C=90°.
（1）若AC=4，BC=3，AE=
，DE⊥AC．且DE=DB，求AD的长；
（2）请你用没有刻度的直尺和圆规，在线段AB上找一点F，使得点F到边AC的距离等于FB(注：不写作法，保留作图痕迹，对图中涉及到的点的用字母进行标注)
参考答案：
【答案】（1）
．（2）作图见解析
【解析】
（1）根据DE∥BC，得出△ADE∽△ABC，进而得到
，据此可得AD的长．
（2）作∠B的平分线BG，交AC于G，作BG的垂直平分线MN，交AB于F，则FG=FB，而FG∥BC，故FG⊥AC，即点F到边AC的距离等于FB．
（1）在Rt△ABC中，AC=4，BC=3，
∴AB=5，
∵DE⊥AC，∠C=90°，
∴DE∥BC，
∴△ADE∽△ABC，
∴，
即
，
解得AD=，
故AD的长为．
（2）如图2所示，作∠B的平分线BG，交AC于G，作BG的垂直平分线MN，交AB于F，则点F即为所求．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，D是△ABC外接圆上的动点，且B，D位于AC的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．
（1）求证：BG∥CD；
（2）设△ABC外接圆的圆心为O，若AB=
DH，∠OHD=80°，求∠BDE的大小．
-
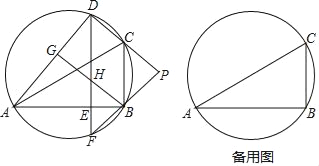
科目： 来源： 题型：
查看答案和解析>>【题目】用适当的方法解下列方程：
（1）4(x-1)2=100
（2）x2-2x-15=0
（3）3x2-13x-10=0
（4）3(x-3)2+x(x-3)=0
-
科目： 来源： 题型：
查看答案和解析>>【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线， DE⊥AB于点E．
（1）如图1，连接EC，求证：△EBC是等边三角形；
（2）点M是线段CD上的一点（不与点C，D重合），以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G．请你在图2中画出完整图形，并直接写出MD，DG与AD之间的数量关系；
（3）如图3,点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G，且MB=MG．试探究ND，DG与AD数量之间的关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司实行年工资制，职工的年工资由基础工资、住房补贴和医疗费三项组成，具体规定如下：
项目
第一年的工资（万元）
一年后的计算方法
基础工资
1
每年的增长率相同
住房补贴
0.04
每年增加0.04
医疗费
0.1384
固定不变
（1）设基础工资每年增长率为x，用含x的代数式表示第三年的基础工资为 万元；
（2）某人在公司工作了3年，他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %，问基础工资每年的增长率是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，图2，图3，在
中，分别以
，
为边，向外作正三角形，正四边形，正五边形，
，
相交于点O.①如图1，求证：
≌
；②探究：如图1，
________；如图2，_______；如图3，_______；（2）如图4，已知：
，
是以为边向外所作正n边形的一组邻边：，
是以为边向外所作正n边形的一组邻边，，的延长相交于点O.①猜想：如图4，
（用含n的式子表示）；②根据图4证明你的猜想.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：配方法是中学数学的重要方法，用配方法可求最大（小）值，对于任意正实数a、b，可作如下变形a+b=
=-2
+2=
+2，又∵≥0，∴ +2≥0+ 2，即a+b ≥2．（1）根据上述内容，回答下列问题：在a+b≥2
（a、b均为正实数）中，若ab为定值p，则a+b≥ 2
，当且仅当a、b满足________时，a+b有最小值2． （2）思考验证：如图1，△ABC中，∠ACB=90°，CD⊥AB，垂足为D，CO为AB边上中线，AD＝2a ，DB＝2b, 试根据图形验证a+b≥2
成立，并指出等号成立时的条件.（3）探索应用：如图2，已知A为反比例函数
的图象上一点，A点的横坐标为1，将一块三角板的直角顶点放在A处旋转，保持两直角边始终与x轴交于两点D、E，F（0，-3）为y轴上一点，连接DF、EF，求四边形ADFE面积的最小值. 
相关试题
