【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值,对于任意正实数a、b,可作如下变形a+b=![]() =
=![]() -2
-2![]() +2
+2![]() =
=![]() +2
+2![]() ,又∵
,又∵![]() ≥0,∴
≥0,∴ ![]() +2
+2![]() ≥0+ 2
≥0+ 2![]() ,即a+b ≥2
,即a+b ≥2![]() .
.
(1)根据上述内容,回答下列问题:在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,则a+b≥ 2
(a、b均为正实数)中,若ab为定值p,则a+b≥ 2![]() ,当且仅当a、b满足________时,a+b有最小值2
,当且仅当a、b满足________时,a+b有最小值2![]() .
.
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a ,DB=2b, 试根据图形验证a+b≥2![]() 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
(3)探索应用:如图2,已知A为反比例函数![]() 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.

参考答案:
【答案】(1)a=b ;(2)当D与O重合时或a=b时,等式成立;(3)28.
【解析】
(1)由给出的材料可知a=b时;
(2)因为AD=2a,DB=2b,所以AB=2a+2b,CO为中线,所以CO=a+b,再利用射影定理得CD=![]() ,在直角三角形COD中斜边大于直角边即CO>CD,问题得证;
,在直角三角形COD中斜边大于直角边即CO>CD,问题得证;
(3)把A点的横坐标为1,代入函数y=![]() 得,y=4,由(2)知:当DH=EH时,DE最小,此时S四边形ADFE=
得,y=4,由(2)知:当DH=EH时,DE最小,此时S四边形ADFE=![]() ×8×(4+3)=28.
×8×(4+3)=28.
(1)a=b,
(2)有已知得CO=a+b,CD=2![]() ,CO≥CD,即
,CO≥CD,即![]() ≥2
≥2![]() .
.
当D与O重合时或a=b时,等式成立.
(3)![]() ,
,
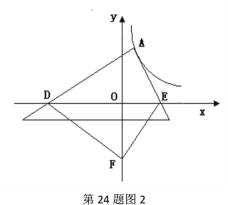
当DE最小时S四边形ADFE最小.
过A作AH⊥x轴,由(2)知:当DH=EH时,DE最小,
所以DE最小值为8,此时S四边形ADFE=![]() (4+3)=28.
(4+3)=28.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC中,∠C=90°.


(1)若AC=4,BC=3,AE=
 ,DE⊥AC.且DE=DB,求AD的长;
,DE⊥AC.且DE=DB,求AD的长; (2)请你用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于FB(注:不写作法,保留作图痕迹,对图中涉及到的点的用字母进行标注)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目
第一年的工资(万元)
一年后的计算方法
基础工资
1
每年的增长率相同
住房补贴
0.04
每年增加0.04
医疗费
0.1384
固定不变
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,图2,图3,在
 中,分别以
中,分别以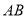 ,
, 为边,向
为边,向 外作正三角形,正四边形,正五边形,
外作正三角形,正四边形,正五边形, ,
, 相交于点O.
相交于点O.①如图1,求证:
 ≌
≌ ;
;②探究:如图1,
 ________;如图2,
________;如图2, _______;如图3,
_______;如图3, _______;
_______;(2)如图4,已知:
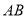 ,
, 是以
是以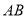 为边向
为边向 外所作正n边形的一组邻边:
外所作正n边形的一组邻边: ,
, 是以
是以 为边向
为边向 外所作正n边形的一组邻边,
外所作正n边形的一组邻边, ,
, 的延长相交于点O.
的延长相交于点O.①猜想:如图4,
 (用含n的式子表示);
(用含n的式子表示);②根据图4证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼成一个等腰三角形(不能有重叠和缝隙).小华的做法是:如图1所示,在矩形ABCD中,分别取AD、AB、CD的中点P、E、F,并沿直线PE 、PF剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2).

(1)在图3中画出另一种剪拼成等腰三角形的示意图;
(2)以矩形ABCD的顶点B为原点,BC所在直线为x轴建立平面直角坐标系(如图4),矩形ABCD剪拼后得到等腰三角形△PMN,点P在边AD上(不与点A、D重合),点M、N在x轴上(点M在N的左边).如果点D的坐标为(5,8),直线PM的解析式为y=kx+b,求所有满足条件的k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:①射线是轴对称图形;②角的平分线是角的对称轴;③轴对称图形的对称点一定在对称轴的两侧;④平行四边形是轴对称图形;⑤平面上两个全等的图形一定关于某条直线对称,其中正确的说法有( )
A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和 都是等边三角形,点
都是等边三角形,点 、
、 、
、 在同一条直线上,
在同一条直线上, 、
、 分别与
分别与 、
、 交于点
交于点 、
、 ,
, 和
和 交于点
交于点 ,有如下结论:①
,有如下结论:① 是等边三角形;②
是等边三角形;② ;③
;③ ≌
≌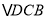 ;④
;④ ;⑤
;⑤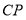 平分
平分 ;⑥
;⑥ ;⑦
;⑦ .其中不正确的结论的个数是( )
.其中不正确的结论的个数是( )
A.
 B.
B. C.
C. D.
D.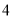
相关试题

