搜索
【题目】如图，某校区内有甲、乙两块大小一样的长方形地块，地块长30m，宽25m，现要在长方形地块内分别修筑如图所示的两条平行四边形小路(图中阴影部分)，余下的部分绿化．现已知ABCD1m，EFGH1m，记甲、乙地块的绿化面积分别为S1、S2，则S1、S2的大小关系是（ ）
A.S1<S2B.S1=S2C.S1>S2D.无法确定
参考答案：
【答案】C
【解析】
根据图片，我们可以看到绿化面积就是长方形的面积减去阴影部分的面积，分别求出两个长方形中阴影部分的面积，就可以得出答案．
解：由题意可知：两个图中左右方向的平行四边形小路的面积都是：30×1=30（m），
两个图中上下方向的平行四边形小路的面积都是：25×1=25（m），
图甲中的重叠部分是1×1=1（m），
，
如图，分别做PR∥CD、NS∥CD交QD于R、S，过点N做NO⊥PR于O，
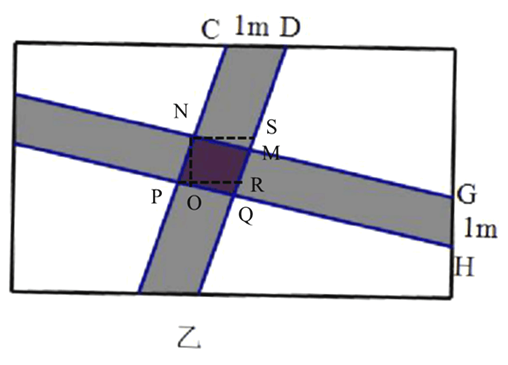
则
，四边形RSNS是平行西边形，
PR=NS=CD=1m，NO＜GH，GH=1m，
在平行四边形PQMN中，PQ∥MN，
，
易证
，
，
，
，
，
；
故答案为：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，点E，F分别在AB，CD上，AF⊥CE，垂足为点O，∠1＝∠B，
∠A+∠2＝90°．求证：AB∥CD．
证明：如图，
∵∠1＝∠B（已知）
∴CE∥BF（同位角相等，两直线平行）
______________
∴∠AFC+∠2＝90°（等式性质）
∵∠A+∠2＝90°（已知）
∴∠AFC＝∠A（同角或等角的余角相等）
∴AB∥CD（内错角相等，两直线平行）
请你仔细观察下列序号所代表的内容：
①∴∠AOE＝90°（垂直的定义）
②∴∠AFB＝90°（等量代换）
③∵AF⊥CE（已知）
④∵∠AFC+∠AFB+∠2＝180°（平角的定义）
⑤∴∠AOE＝∠AFB（两直线平行，同位角相等）
横线处应填写的过程，顺序正确的是（ ）
A.⑤③①②④B.③④①②⑤C.⑤④③①②D.⑤②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，对于点P(x，y)，我们把P1(y1，x1)叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，，这样依次得到各点．若A2020的坐标为(3，2)，设A1(x，y)，则xy的值是（ ）
A.-5B.-1C.3D.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=AC，∠BAC=45°，BC=2，D是线段BC上的一个动点，点D是关于直线AB、AC的对称点分别为M、N，则线段MN长的最小值是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
+ 
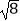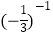﹣|2sin45°﹣1|． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，△ABC的三个顶点的位置如图所示．现将△ABC平移，使得点A移至图中的点A'的位置．
（1）平移后所得△ABC的顶点B的坐标为 ，C的坐标为 ；
（2）平移过程中△ABC扫过的面积为 ；
（3）将直线AB以每秒1个单位长度的速度向右平移，则平移 秒时该直线恰好经过点C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，AB∥CD，点M为直线AB，CD所确定的平面内的一点，若∠A105，∠M108，请直接写出∠C的度数 ；
（2）如图2，AB∥CD，点P为直线AB，CD所确定的平面内的一点，点E在直线CD上，AN平分∠PAB，射线AN的反向延长线交∠PCE的平分线于M，若∠P30，求∠AMC的度数；
（3）如图3，点P与直线AB，CD在同一平面内，AN平分∠PAB，射线AN的反向延长线交∠PCD的平分线于M，若AMC180
P，求证：AB∥CD．
相关试题
